
|
teoria
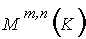 |
|
Torna alla teoria |
I
l
gruppo abeliano
delle
Matrici :
|
||
| ||||
L'operazione + Ŕ la
somma tra matrici, che gode delle seguenti proprietÓ:
|
 L'operazione di somma tra matrici Ŕ chiusa . Infatti la somma di due matrici Ŕ ancora una matrice.  L'operazione di somma tra matrici Ŕ associativa . Infatti gli elementi delle matrici sono elementi di un campo, in cui vale la proprietÓ associativa.  Rispetto all'operazione di somma tra matrici 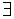 l' elemento neutro
: l' elemento neutro
:la matrice nulla.  Rispetto all'operazione di somma tra matrici 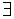 l' elemento inverso
: l' elemento inverso
:se 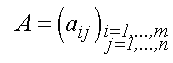 allora allora 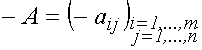 Ŕ la
Ŕ la matrice inversa.  L'operazione di somma tra matrici Ŕ commutativa . Infatti gli elementi delle matrici sono elementi di un campo, in cui vale la proprietÓ commutativa. |