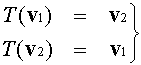Consideriamo il piano p generato dai vettori linearmente indipendenti v₁, v₂.
Poiché

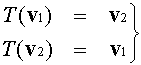T(T(v₁)) = v₁, T(T(v₂)) = v₂.

Quindi l'applicazione, ristretta al piano p è tale che se viene applicata due volte si ottiene l'identità su p, cioè :

L'applicazione può essere o una simmetria rispetto ad una retta o una rotazione di 180°. Quest'ultima è da escludere in quanto " vÎ p si ottiene sempre il vettore opposto, cioè T(v₁) = -v₁, e in questo caso i vettori sono linearmente dipendenti.
Consideriamo la simmetria rispetto una retta.
Occorre prendere come vettori v₁, v₂, linearmente indipendenti, due vettori che non stiano né sull'asse di simmetria né su una retta ad essa perpendicolare. Infatti i simmetrici di quei vettori v _i che giacciono sull'asse di simmetria sono i vettori stessi, quindi si ha l = 1 e i v _i e i loro trasformati, coincidendo, sono linearmente dipendenti. Analogamente al caso della rotazione di 180°, l'applicazione manda quei vettori w_i che stanno su una retta perpendicolare all'asse di simmetria nei vettori opposti (l = -1) , che con i w_i sono linearmente dipendenti.