La risposta è esatta!
La risposta è esatta!
| F(1, 0, 0, 0) = (1, 1, 1) | F(0, 1, 0, 0) = (-1, 0, 1) |
| F(0, 0, 1, 0) = (1, 2, 3) | F(0, 0, 0, 1) = (1, -1, -3) |
Quindi la matrice A che rappresenta la F, cioè avente per righe i generatori di Im(F), è :
A = | che ridotta con il metodo di eliminazione di Gauss |
diviene :
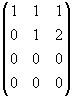
Quindi dim Im(F) = 2. Una base per Im(F) è per esempio : {(1, 1, 1), (0, 1, 2)} .
Il Ker(F) è dato dalle soluzioni del sistema omogeneo A ×X = 0, cioè :
 |  |  |
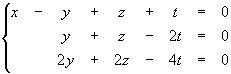Le variabili libere sono z e t, quindi dim Ker(F) = 2.
Poniamo z = -1, t = 0 per avere la soluzione (2, 1, -1, 0), z = 0, t = 1 per avere la soluzione (1, 2, 0, 1).
Così {(2, 1, -1, 0), (1, 2, 0, 1)} è una base di Ker(F).
Si noti che dim Im(F) + dim Ker(F) = 2 + 2 = 4, che è la dimensione del dominio R4 di F.
,