Soluzione

  1. Poiché la matrice è triangolare gli autovalori di A sono i suoi elementi diagonali. Infatti il polinomio caratteristico è:

    2. PA(l) = (l - l)(m - l)(n - l) = 0

    e quindi gli autovalori sono: l = l, l = m, l = n.

  2. Siano A, BÎ H3(R). Mostriamo che ABÎ H3(R), e che quindi l'operazione di prodotto tra matrici è interna.

    3. Infatti siano:

    A = 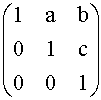, B =

    AB = 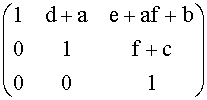Î H3(R).

    Inoltre se A, B, C Î H3(R) si ha (AB)C = A(BC), poiché il prodotto tra matrici gode della proprietà associativa.

    " A Î H3(R) esiste l'elemento neutro, che è la matrice identità, dove IÎ H3(R), infatti:

    I = 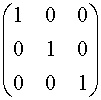Î H3(R).

    Verifichiamo infine che " A Î H3(R) $ A- 1Î H3(R): AA- 1 = A- 1A = I

    Infatti:

    se A = 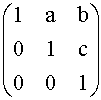, A- 1 = 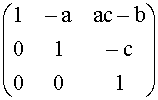Î H3(R).

    Quindi H3(R) è un gruppo rispetto alla moltiplicazione di matrici.

    Il polinomio caratteristico di AÎ H3(R) è:

    PA(l ) = (1- l )3

    quindi 1 è l'unico autovalore di A con molteplicità 3.

    Troviamo una base dell'autospazio V1 relativo all'autovalore 1.

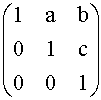
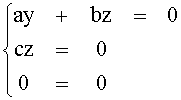    = Û Û

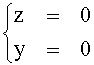
    Il sistema ha soltanto una variabile libera, quindi dim V1= 1. Una base dell'autospazio può essere trovata ponendo, per esempio, x = 1, cioè { (1, 0, 0)} . Poiché m1 = 3 ¹ 1 = dim V1, A non può essere diagonalizzata. Affinché A sia diagonalizzabile ci deve essere un autospazio di dimensione 3, che si ottiene con 3 variabili libere. Quindi solo nel caso in cui a = b = c = 0, cioè gli unici elementi diagonalizzabili in H3(R) sono le matrici identità.

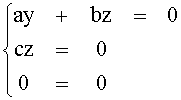  3. Determiniamo il KerT, risolvendo il sistema T(x, y, z) = (0, 0, 0), cioè

    Û

    Essendoci una sola variabile libera dim KerT = 1 e una base può essere { (1, 0, 0)}.
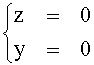
    Determiniamo l'immagine di T. La matrice A determina un'applicazione lineare la cui immagine è generata dalle colonne di A. Poiché è già ridotta a gradini, si ha rgA = dim Im T = 2. Una base dell'immagine può essere: { (a, 0, 0), (b, c, 0)} .
    Ma allora la relazione R3 = KerT Å ImT non è verificata in quanto KerT Ç ImT = (a, 0, 0) ¹ 0.