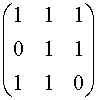
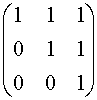I tre vettori sono linearmente indipendenti in quanto la matrice da essi formata ha rango uguale a 3. Infatti riduciamola in forma triangolare con il metodo di eliminazione di Gauss:

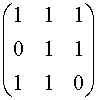
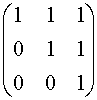Inoltre, essendo dim R³ = 3 essi formano una base.

1. F(1, 1, 1) = (1, 0, -1) = 0 (1, 1, 1) + 1 (1, 1, 0) - 1 (0, 1, 1)

   F(1, 1, 0) = (-1, 0, 0) = -1 (1, 1, 1) + 0 (1, 1, 0) + 1 (0, 1, 1)

   F(0, 1, 1) = (0, 0, 1) = 1 (1, 1, 1) - 1 (1, 1, 0) + 0 (0, 1, 1)

   quindi

   M_v(F) = .

   Determiniamo il KerF risolvendo il sistema M_v(F)X = 0, cioè

   

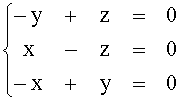
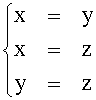
   Poiché c'è una sola variabile libera dim KerF = 1, e una base può essere data dal vettore { (1, 1, 1)} . L'immagine di F: R³® R³ è generata dalle colonne di M_v(F). Formiamo la matrice avente per righe i generatori di ImF e riduciamola per righe nella forma a gradini con il metodo di eliminazione di Gauss:

   .

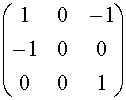
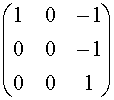
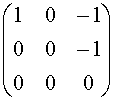   Quindi dim ImF = 2 e una base è data da { (1, 0, -1), (0, 0, -1)} .

2. Calcoliamo il polinomio caratteristico e troviamo gli autovalori:

   P(l ) = det[M_v(F) - l I] = 0

    

   Û det= 0 Û l ³ + 3l = 0 Û l (l ² + 3) = 0

   Consideriamo due casi:

   • Se M_v(F) viene considerata come matrice nel campo reale, allora ha unicamente l'autovalore l = 0. Poiché 0 ha solo un autovettore indipendente ( dim V₀ = dim Ker F = 1), allora M_v(F) non è diagonalizzabile.
   • Se, invece, M_v(F) viene vista nel campo complesso, possedendo tre autovalori distinti, cioè l ₁ = 0, l ₂ = - , l ₃ = + , essa è diagonalizzabile.

 

3. M_e(F) = M_e,v(1_V) M_v(F) M_v,e(1_V)

   Determiniamo M_e,v(1_V):

   (1, 0, 0) = 1 (1, 1, 1) + 0 (1, 1, 0) - 1(0, 1, 1)

   (0, 1, 0) = -1 (1, 1, 1) + 1 (1, 1, 0) + 1(0, 1, 1)

   (0, 0, 1) = 1 (1, 1, 1) - 1 (1, 1, 0) + 0 (0, 1, 1).

   Quindi

   M_e,v(1_V) = .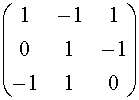

   Analogamente determiniamo M_v,e(1_V):

   (1, 1, 1) = 1 (1, 0, 0) + 1 (0, 1, 0) + 1(0, 0, 1)

   (1, 1, 0) = 1 (1, 0, 0) + 1 (0, 1, 0) + 0(0, 0, 1)

   (0, 1, 1) = 0 (1, 0, 0) + 1 (0, 1, 0) + 1(0, 0, 1)

   quindi

   M_v,e(1_V) = .

   Allora

   A = M_e(F) = = .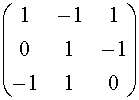

4. B = .

   Poiché B = M_v(F) allora A e B sono simili, in quanto rappresentano lo stesso operatore lineare rispetto basi diverse.