Sia V uno spazio vettoriale sul campo K, dim (V) = n.
Un operatore F Î End(V) si dice diagonalizzabile se esiste una base e di V tale che Me(F) sia una matrice diagonale, cioè della forma
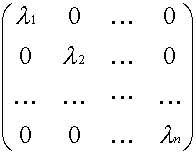
per opportuni l
1,l
2, … , l
n Î K.
Se ciò avviene e è una base diagonalizzante per F.
Se F : V ® V è un operatore lineare diagonalizzabile ed e una base diagonalizzante per F, si ha :
F(e1) =l
1 e1, F(e2) = l
2 e2, ... , F(en) =l
n en, cioè ogni vettore della base viene mandato in un multiplo di sé.
Questo significa che gli ei sono autovettori per F.