 La risposta è esatta !
La risposta è esatta ! La risposta è esatta !
La risposta è esatta !
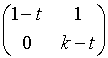 = (1 - t)(k - t),
= (1 - t)(k - t),
Per k ¹ 1, A ha due autovalori distinti, e quindi ci sono due autovettori indipendenti, cosicché A è diagonalizzabile.
Se K = 1, l
= 1 è l'unico autovalore, e dobbiamo vedere quanto vale dim V1.
Gli autovettori sono le soluzioni del sistema :
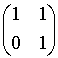
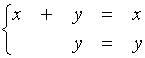
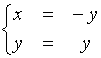
quindi V1 = {(-y, y)}, ed una base di V1 è data dal vettore (-1, 1), perciò dim V1 = 1, ed A non è diagonalizzabile in quanto possiede al pił un autovettore indipendente.