A = 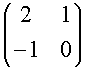 .
.
Applichiamo F ai vettori della base canonica :
| F(1, 0) = (2, -1), | F(0, 1) = (1, 0). |
Quindi la matrice A, associata all'applicazione lineare rispetto alla base canonica, è :
A = 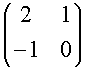 .
.
Per trovare gli autovalori dobbiamo calcolare :
det(A -t I) = det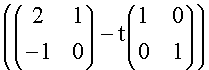 = det
= det 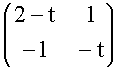 =
=
Quindi gli autovalori sono le soluzioni dell'equazione :
t2 - 2t + 1 = 0, | cioè | (t - 1)2 = 0 | Þ | t = 1. |
L'unico autovalore è perciò l = 1.
Gli autovettori corrispondenti sono le soluzioni del sistema
A× X = 1× X =X :
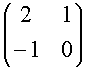
![]() =
= ![]()
![]()
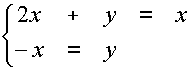
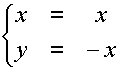
Si ha allora : V1 = {(x, -x) : x Î R} Í R2 e dim V1 = 1.