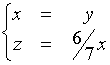Chiamando x, y e z le quantità di conigli immesse nelle tre zone, si avrà :
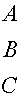
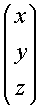
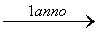
 =
= 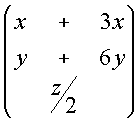
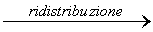
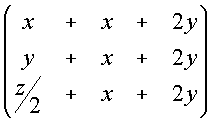 =
= 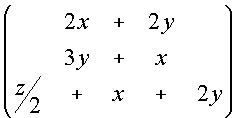
Quindi si ha un'applicazione lineare F : R3 ® R3, di matrice
M = 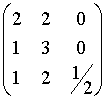 .
.
Poiché se X è la colonna delle distribuzioni iniziali, si vuole che la distribuzione dopo un anno sia del tipo l
X, proporzionale ad X, quello che cerchiamo sono gli autovalori e gli autovettori di M.
Il polinomio caratteristico di M sarà :
P(t) = det(M - tI) = 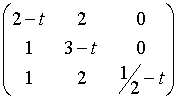 ;
;
sviluppando rispetto all'ultima colonna si ha :
P(t) =(1/2 - t)[(2 - t)(3 - t) -2] = (1/2- t)(t2 - 5t + 4).
Ponendo P(t) = 0 si trovano le soluzioni :
| l
1 = 1/2, | l
2 = 1, | l
3 = 4. |
Cerchiamo i rispettivi autovettori :
 l
= 1/2
l
= 1/2
Si ha : (M - l
1I) = 0, e cioè :
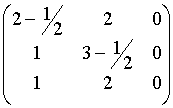
 =
= 

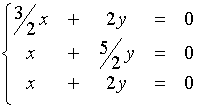

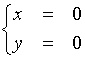
Quindi l'autospazio è : V1/2 = {(0, 0, z)}.
 l
= 1 :
l
= 1 :
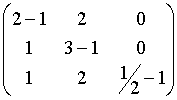
 =
= 

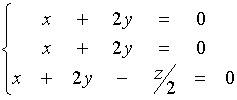


Quindi l'autospazio è : V1 = {(-2y, y, 0)}.
 l
= 4 :
l
= 4 :
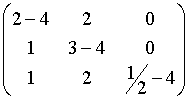
 =
= 



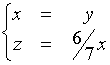
Quindi l'autospazio è : V4 = {(x, x, 6/7x)}.
Vediamo ora di interpretare questi risultati alla luce del nostro problema.
L'autovalore l
1 = 1/2 , con gli autovettori (0, 0, z) ci danno una possibile soluzione del nostro problema : immettere tutti i conigli nella sola area C.
Ma questa non è una soluzione ottimale per i cacciatori : infatti, per il primo anno avrebbero a disposizione molta selvaggina cacciabile, ma essa si dimezzerebbe ogni anno, e dopo poco la popolazione diverrebbe irrisoria.
L'autovalore l
2 = 1 non dà nessuna soluzione per il nostro problema, infatti l'autovettore (-2y, y, 0) non ha alcun interesse, poiché non possiamo immettere in una zona una quantità di conigli negativa!
Quindi l'ultima speranza per i nostri cacciatori è l'autovalore l
3 = 4, con l'autovettore (x, x,6/7x). Poiché la quantità totale immessa deve essere 800, dovremo avere :
x + x + 6/7x = 800, e cioè 202/7x= 800, x = 280.
Quindi questa è la soluzione ottimale per i cacciatori : immetteranno 280 conigli rispettivamente nelle aree A e B, e 240 nell'area C. Dopo un anno la popolazione totale sarà quadruplicata, e nella zona C ci saranno ben 960 conigli da cacciare.
![]()
![]()
![]()
 =
= 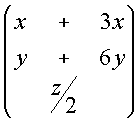
![]()
![]()
![]()
 =
= 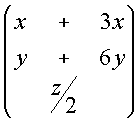
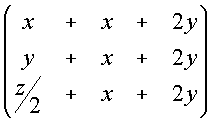
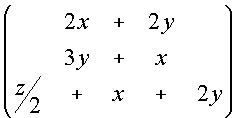
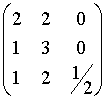 .
.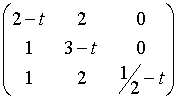 ;
; l
= 1/2
l
= 1/2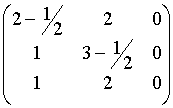
![]() =
= ![]()
![]()
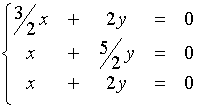
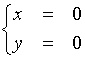
 l
= 1 :
l
= 1 :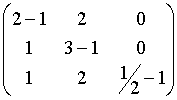
![]() =
= ![]()
![]()
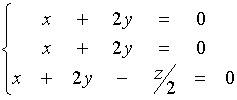

 l
= 4 :
l
= 4 :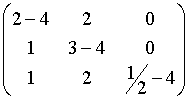
![]() =
= ![]()
![]()