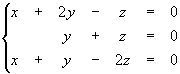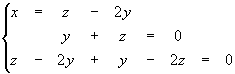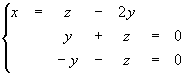1. Calcoliamo F sui vettori della base canonica :

    2. F (1, 0, 0) = (1, 0, 1), F (0, 1, 0) = (2, 1, 1) F (0, 0, 1) = (- 1, 1, - 2)

    La matrice che rappresenta la F ha per righe i generatori di Im(F) . Con il metodo di eliminazione di Gauss riduciamola in forma triangolare superiore:

     

    		 in 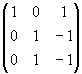in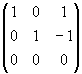

    Quindi {(1, 0, 1), (0, 1, - 1)} è una base di Im(F) e dim Im(F) = 2.

  2. Determiniamo i vettori tali che F (x, y, z) = (0, 0, 0), ovvero

F (x, y, z) = (x + 2y – z, y + z, x + y – 2z) = (0, 0, 0)

Uguagliando le componenti corrispondenti a due a due si forma il sistema omogeneo il cui spazio soluzione è il nucleo di F, Ker(F) :

 

 ovvero

 

 ovvero

 


La sola variabile libera è z, quindi dim Ker(F) = 1.
Sia z = 1, allora {(3, -1, 1)} è una base di Ker(F).
(Notare che dim Im(F) + dim Ker(F) = 2 + 1 = 3, che è la dimensione del dominio R3 di F.)