1. Siano V = R⁴ e W = R³ due spazi vettoriali e sia

    

   A_k = .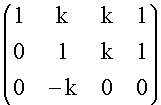

   1. Determinare Ker A_k al variare di k Î R.
   2. Determinare Im A_k e Im A_k Ç U, dove U = á (1, 0, 1), (-1, 1, 1)ñ al variare di kÎ R ( si osservi che siamo in W).

 

2. Sia V = R₃[x] lo spazio vettoriale dei polinomi in una indeterminata di grado £ 3 e sia T : V ® V l'applicazione lineare così definita :

   T(p(x)) = p(1 - x) ovvero

   T(a₀ + a₁x + a₂x² + a₃x³) = a₀ + a₁(1 - x) + a₂(1 - x)² + a₃(1 + x)³ con a_i Î R

   Stabilire se T è diagonalizzabile determinandone tutti gli autospazi.

Siano V = M^2,3(R) e sia T_k : V® V la trasformazione lineare che agisce nel seguente modo :

1. Determinare W = Ker T_k e Im T_k al variare di k Î R.
2. Stabilire se T_k è diagonalizzabile e per quali valori di k Î R.
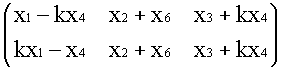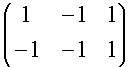3. Stabilire se la matrice A = appartiene ad Im T_k per qualche k e per k = -1 determinarne la preimmagine.

1. Sia V = R₃[x] e sia T : V ® V l'applicazione definita nel modo seguente:

   " p(x) Î V,

   T(p(x)) = p(x) - xp'(x) + x²p''(x)

   1. Stabilire se T è una trasformazione lineare.
   2. Determinare KerT ed ImT.
   3. Stabilire se T è diagonalizzabile.
   4. Determinare la retroimmagine di 1 + x + x².

 

2. Sia V = R₃[x] e sia W = M²(R). Sia poi data l'applicazione T : V ® W tale che

    

   T(p(x)) = .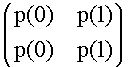

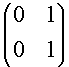
   1. Stabilire se T è una trasformazione lineare e se è un isomorfismo.
   2. Determinare KerT ed ImT.
   3. Determinare la retroimmagine di A =
   .

 

3. Sia V = R³ e sia T : V ® V un endomorfismo.

   Siano a = { x Î V/ x₂= 0} , b = { x Î V/ x₃= 0} e sia s = { x Î V/ x₁ + x₂ - x₃= 1} .

   Stabilire per ciascuna delle seguenti affermazioni se è vera o falsa giustificando appropriatamente la risposta:

   1. Se s Í KerT allora T = 0.
   2. Se a Í Vl e se b Í Vm dove l e m sono autovalori reali di T allora l = m e T = l I.
   3. T possiede sempre un autovalore reale.

 

 

4. Sia V = R₃[x] e sia T : V ® V l'applicazione definita nel modo seguente:

   " p(x) Î V,

   T(p(x)) = p(x) + p'(x) - 2xp''(x)

   1. Stabilire se T è una trasformazione lineare.
   2. Determinare KerT ed ImT.
   3. Stabilire se T è diagonalizzabile.
   4. Determinare la retroimmagine di 1 + x².