Corso di Laurea in Ingegneria

Prova d'esame del 4/11/97

 

  1. Sia data la seguente matrice :

     

    B =

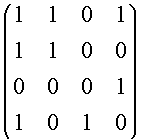
    ed i quattro vettori di V = R4:

    u1 = (1, 1, 1, 0) t, u2 = (-1, 1, 0, 1) t, u3 = (-1, 0, 0, 1) t, u4 = (1, 0, 0, 0) t.

    Sia T : V ® V la trasformazione lineare che ammette B come matrice rispetto la base u1, u2, u3, u4.

    1. Determinare KerT ed Im T;
    2. Stabilire se T è diagonalizzabile e/o se ammette una base ortonormale di autovettori.

    2.  

     

     

  2. Per ciascuna delle seguenti affermazioni dire se è vera o falsa giustificando appropriatamente la risposta.

    Siano V e W spazi vettoriali sul campo K di dimensione n ed m rispettivamente.

    1. Hom(V, W) contiene isomorfismi se e solo se m = n.
    2. Se f Î Hom(V, W) e m > n, Im (f ) Ì W.
    3. Se f Î Hom(V, W) e n > m, Ker (f ) ¹ 0.

 

 

Prova d'esame del 9/6/97

  1. Sia V = M3,3(R) e sia T : V® V l'applicazione definita nel modo seguente :

    " A Î V :

    T(A) = - tr(A)I + A

     

    1. Stabilire se T è una trasformazione lineare.
    2. Determinare Ker T ed Im T .
    3. Stabilire se T è diagonalizzabile.

    2.  

     

  2. Sia V = R3[x] e siano dati i seguenti polinomi :

    p0 = -1, p1 = -1 - x, p2 = -1 - x - x2, p3 = -1 - x - x2 - x3.

    Sia poi data la trasformazione lineare T : V® V tale che :

    T(1) = -1 - x, T(1 + x) = 1 + x + x2, T(x2) = x3, T(x3) = -x - x2 - x3.

    1. Determinare la matrice associata a T rispetto la base p0, p1 , p2 , p3.
    2. Stabilire se T è diagonalizzabile.
    3. Se D : V® V indica la derivazione, stabilire se DT è diagonalizzabile.