se non interessa la dimostrazione

Consideriamo la circonferenza goniometrica e su di essa consideriamo gli angoli m, b, m-b :  

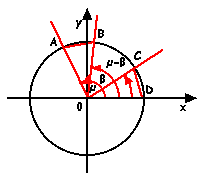
E' evidente dal disegno che i segmenti AB e CD sono uguali, si avrà quindi:
AB² = CD²
si vede inoltre che le coordinate dei loro estremi sono:
A=( cosm , sinm ) ;

B=( cosb , sinb ) ;

C=( cos(m-b) , sin(m-b) ) ;

D=( 1 , 0)
per la formula della distanza fra due punti si otterrà:

AB² = ( cosm - cosb )² + ( sinm - sinb )²

e,analogamente:

CD² = ( cos(m-b) - 1 )² + ( sin(m-b) - 0 )²

e,di conseguenza:

(cos(m-b)-1)² +(sin(m-b)-0)² =(cosm-cosb)² +(sinm-sinb)²

svolgendo i quadrati si otterrà:

cos²(m-b) + 1 - 2cos(m-b) + sin²(m-b) - 2sin(m-b) =

= cos²m + cos²b - 2cosmcosb + sin²m + sin²b - 2sinmsinb

da cui, tenendo presente la relazione fondamentale della goniometria:

1 + 1 - 2cos(m-b) = 1 + 1 - 2cosmcosb - 2sinmsinb

e,finalmente:

 
Per quanto riguarda la formula del seno si osservi che:

sin(m-b) = cos(p/2 - (m-b)) = cos((p/2 +b)-m)

quindi, applicando a questa la formula del coseno della differenza di due angoli sopra trovata,e ricordando le formule degli archi associati si avrà:

sin(m-b) = cos(p/2 - (m-b)) = cos((p/2 + b)- m) = cos(p/2 + b)cosm + sin(p/2 + b)sinm =

= -sinbcosm + cosbsinm

quindi la formula cercata è:

Per quanto riguarda le formule di sottrazione per la tangente e la cotangente, esse si ricavano con semplici passaggi direttamente da queste e sono:  

tg(m-b) = sin(m-b)/cos(m-b)=(sinmcosb - cosmsinb)/(cos(m-b) cosmcosb + sinmsinb)

naturalmente è importante supporre cosm e cosb entrambi diversi da zero, dividendo poi numeratore e denominatore cosmcosb e semplificando opportunamente si ha :

e analogamente :