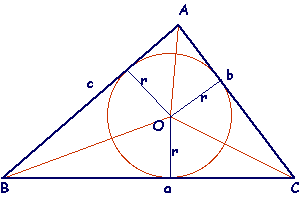
in essa sono posti in evidenza i raggi che coincidono con le distanze del centro dai lati. L'area A del triangolo ABC è uguale alla somma delle aree dei triangoli che in esso compaiono cioè:
A = AOB + AOC + COB =
= ar/2 + br/2 + cr/2 =
= (a + b + c)r/2 = pr (p è sempre il semiperimetro)
quindi la misura del raggio è data da:

moltiplicando e dividendo numeratore e denominatore per (p-a), si ottiene:

Circonferenza CIRCOSCRITTA (il centro O è il punto d'incontro degli assi e si chiama CIRCOCENTRO)

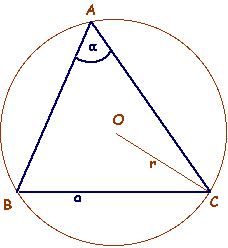
Dato un triangolo e note la misura di un suo lato a e l'ampiezza a dell'angolo opposto, la misura r del raggio della circonferenza circoscritta è:

questo è diretta conseguenza del teorema della corda.
Se, dato un triangolo, sono note le misure dei suoi tre lati a,b,c, la misura del raggio r della circonferenza circoscritta è:

Per dimostrarlo sarà sufficiente moltiplicare numeratore e denominatore della formula precedente per bc, ottenendo:

e quindi, per la prima delle formule di calcolo dell'area di un triangolo:

Circonferenza EXINSCRITTA (è la circonferenza tangente ad un lato del triangolo e ai prolungamenti degli altri due):
Dalla seguente figura

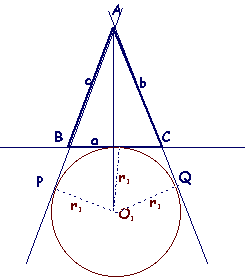
è evidente che il centro di questa circonferenza è il punto d'incontro delle bisettrici degli angoli BAC, PBC e BCQ.
Per quanto riguarda l'area invece
A_ABC = A_ABO1 + A_ACO1 - A_BCO1
Sostituendo quindi le corrispondenti misure:

da cui:

Analogamente: