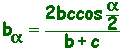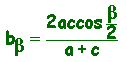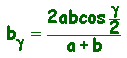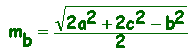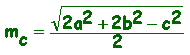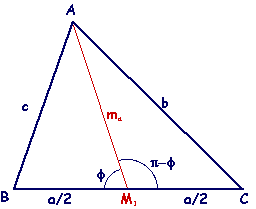
del triangolo ABC si conoscono le misure a, b, c dei tre lati, mentre m_a , misura della mediana AM₁ , è ciò che si deve trovare. Applicando il teorema del coseno al triangolo AM₁B e poi ad AM₁C, si trova:
c² = a²/4 + m_a² - a m_a cosf
b² = a²/4 + m_a² + a m_a cosf
sommando queste due uguaglianze membro a membro si ottiene:
b² + c² = a²/2 + 2 m_a²
da cui:
e, analogamente:

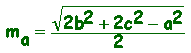
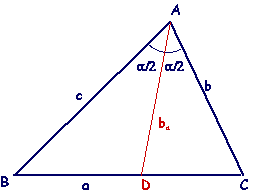
di questo triangolo siano note le misure dei lati b e c e l'ampiezza dell'angolo a tra essi compreso.
E' evidente che vale:
A_ABC = A_BAD + A_ADC
che è equivalente scrivere nella forma:

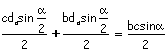
che, per la formula di duplicazione del seno, diventa:

dividendo primo e secondo membro per sin(a/2) (si può certamente fare perché sicuramente diverso da zero), si ha:

e quindi:
Analogamente: