Sono equazioni del tipo asinx + bcosx = c , con a, b, c numeri reali assegnati, che supporremo diversi da zero (infatti nel caso in cui a o b fossero uguali a zero si avrebbe di nuovo un'equazione elementare, il caso in cui c sia uguale a zero verrà esaminato più avanti).Per risolvere questo tipo di equazioni conviene sostituire sinx e cosx con le loro corrispondenti espressioni razionali in funzione di tg(x/2) valide, come si è visto in precedenza per x p + 2kp, si avrà quindi:

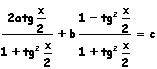
svolgendo i calcoli si otterrà l'equazione di secondo grado in tg(x/2):

(b + c)(tg(x/2))2 - 2atg(x/2) + c - b = 0

(1)

se questa avrà due soluzioni reali, le chiameremo r₁ e r₂ , si avranno le seguenti equazioni elementari, di cui si conosce la soluzione:

tg(x/2) = r1

tg(x/2) = r2

Per l'equazione lineare data potrebbero essere però soluzioni anche i valori del tipo x = p + 2kp, che non si possono avere col metodo descritto a causa delle restrizioni imposte dalle formule usate; se però si verifica il caso in cui b + c = 0 , si ha un'equazione di primo grado intera intg(x/2) al posto della (1) di cui x = p + 2kp sono soluzioni.