ESEMPI DI IDENTITA' GONIOMETRICHE CONDIZIONATE

esempio 1; esempio 2;

• Risolvere l'equazione

innanzitutto occorre imporre:

b kp con k = + 1, + 2, + 3,...

difatti per questi valori non esiste la ctg, dopodiché si sviluppano i due membri dell'uguaglianza (quest'operazione verrà qi fatta separatamente per i due membri al solo scopo di semplificare le cose):

1° membro	= sin(2p - b) cos(p - b) ctgb =
	= -sinb (-cosb) = cos2b
2° membro	= 1 + cos(p/2 - b) cos(p/2 + b) =
	= 1 + sinb (- sinb) =
	= 1 - sin2b = cos2b = 1° membro

Concludendo quindi si dirà che questa identità è verificata per tutti i valori dell'angolo b tranne kp.

INIZIO PAGINA

• Risolvere l'equazione = cos²b (1 + tgb)

  le condizioni da imporre questa volta saranno due:

  b p/2 + kp con k = + 1, + 2, + 3,...

  in quanto per tali valori la tg non esiste;

  b p/4 + kp con k = + 1, + 2, + 3,...

  sviluppiamo ora i due membri come nell'esempio precedente:

  1° membro	= =
  	= =
  	= =
  	= (cosb - sinb) (cosb + sinb) =
  	= (cosb + sinb) cosb
  2° membro	= cos2b (1 + tgb) =
  	= cos2b =
  	= cos2b =
  	= cosb (cosb + sinb) = 1° membro

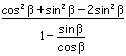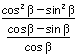  Perciò si dirà che l'identità è verificata per tutti i valori di b esclusi p/2 + kp e p /4 + kp.

  INIZIO PAGINA