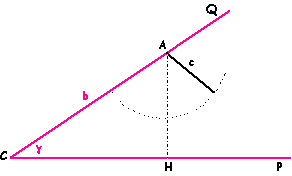
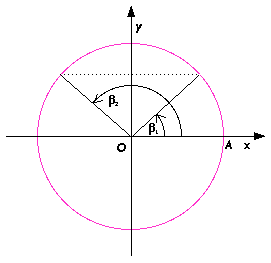
g
< p/2
Se c < b deve essere g
< b;
perciò sono accettabili entrambi i valori di
b
poiché vale
g +
b1
< p
e
g +
b2
< p
Esisteranno
perciò due triangoli soddisfacenti il
problema:
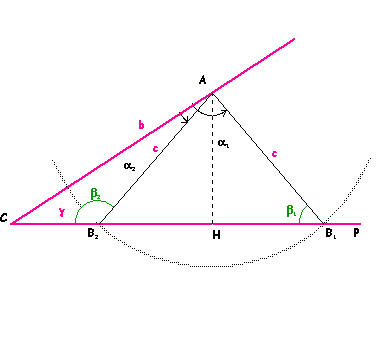
da
questa figura risulta che la circonferenza di centro A e raggio
c (con bsing
< c < b) interseca il lato CP nei due punti B1
e B2, si ottengono così due triangoli:
AB1C e AB2C in corrispondenza dei due
angoli.
Si consideri in primo luogo il triangolo AB1C,
in esso si ha a1
= p
- (g
+
b1)
applicando il teorema dei seni si ottiene:
a/sina1
= c/sing
, da cui a = csina1/sing
;
in AB2C si ha a2
= p
- (g
+
b2)
e, sempre per il teorema dei seni
a/sina2
= c/sing
, da cui a = csina2/sing
;
se c = b si ha b
= g,
perciò l'angolo ottuso b2
non può risolvere il problema in quanto
g
+ b2
= p.
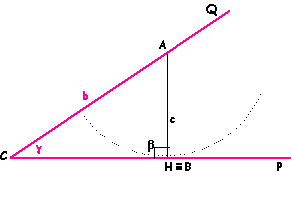
Il problema ha una sola soluzione, in questo caso il triangolo
è isoscele (vedi figura seguente)
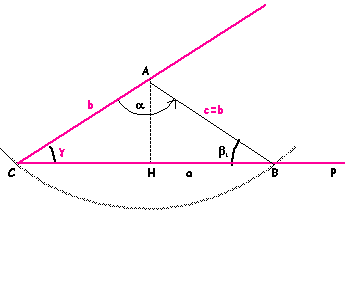
la
circonferenza di centro A e raggio c, infatti, è tale
che b sing
< c = b, e incontra il lato CP in C e B, generando in questo
modo un triangolo isoscele sulla base CB.
Si trova a
= p
- (g
+
b1)
e, sempre per il teorema dei seni:
a/sina
= c/sing
, da cui a = csina/sing
.
Se c > b si ha g
> b,
perciò l'angolo ottuso b2
non può risolvere il problema in quanto
g
+ b2
> p,
si
ha quindi un solo triangolo.
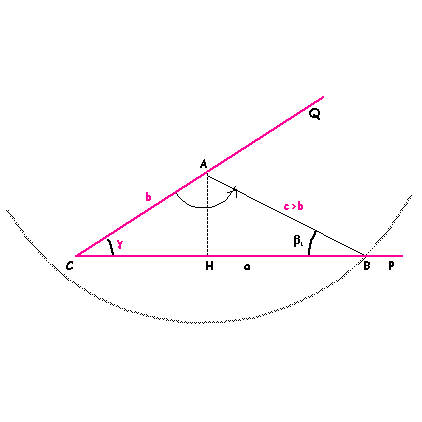
Come
si vede nella figura qui sopra la circonferenza di centro A e
raggio C è tale per cui :
bsing
< b < c;
interseca quindi il lato CB in un solo punto, B, originando
quindi un solo triangolo per il quale vale:
a
= p
- (g
+
b1)
da cui
a = csina/sing
![]()
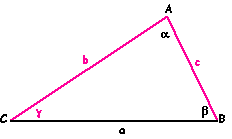
![]() (altrimenti si ritroverebbe un caso già visto), si supponga
inoltre che il triangolo sia scaleno;
(altrimenti si ritroverebbe un caso già visto), si supponga
inoltre che il triangolo sia scaleno;