tgx
<
Si
ricercano innanzitutto le soluzioni positive e non superiori
all'angolo piatto dell'equazione goniometrica elementare tgx =
, ovviamente saranno esclusi i valori per i quali la tangente non
è definita (nella figura sono segnati da una crocetta
rossa).
Queste
soluzioni sono:
x
= 
e x = 
A
questo punto si disegna la circonferenza goniometrica e la retta
tangente alla circonferenza nel punto A, su di essa si fisserà
il punto T di ordinata
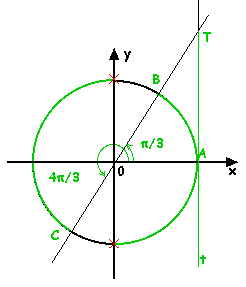
Detti
B e C i punti d'ntersezione della retta OT con la circonferenza, si
avranno i due angoli orientati da cui si ricava la soluzione della
disequazione data:
< x <
Ricordando
poi che la funzione tgx è periodica di periodo
p,
si avrà che le soluzioni sono tutti e soli i valori appartenti
agli intervalli:
+ kp
< x <
+ kp
(con
k = 0; +1; + 2; + 3;...)