L'area di un quadrilatero qualsiasi è uguale al semiprodotto delle misure delle diagonali per il seno di uno degli angoli fra esse compreso:

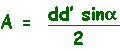
Si consideri la seguente figura:

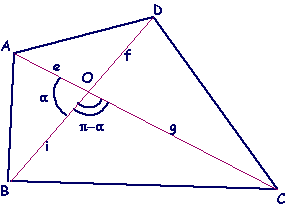
Questo quadrilatero, come è evidente, non ha particolari proprietà, le sue diagonali sono AC e DB e misurano rispettivamente e + g e i + f.
L'area A del quadrilatero è data dalla somma delle aree dei quattro triangoli AOD, DOC, BOC, AOB:
A = (ef sin(p - a))/2 + (fg sina)/2 + (ig sin(p - a))/2 + (ei sina)/2 =

= (ef sina)/2 + (fg sina)/2 + (ig sina)/2 + (ei sina)/2 =

= (sina (ef + fg + ig + ei))/2 =

= (sina(e(f + i) + g(f + i)))/2 =

= (sina (e + g) (i + f))/2

ponendo infine d = e+g e d' = i+f
si ottiene la formula cercata.