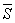 1, si ha S1 è contenuto in
1, si ha S1 è contenuto in 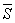 1; sia ora x Ï S1, allora x è compreso tra due numeri interi consecutivi: n < x < n+1, posto e = min(x-n; n+1-x), nel disco De
(x) non cade alcun punto di S1, quindi xÏ
1; sia ora x Ï S1, allora x è compreso tra due numeri interi consecutivi: n < x < n+1, posto e = min(x-n; n+1-x), nel disco De
(x) non cade alcun punto di S1, quindi xÏ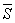 1, si conclude che
1, si conclude che 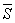 1 = S1.
1 = S1.Risoluzione dell'Esercizio 1
Determiniamo 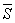 1, si ha S1 è contenuto in
1, si ha S1 è contenuto in 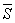 1; sia ora x Ï S1, allora x è compreso tra due numeri interi consecutivi: n < x < n+1, posto e = min(x-n; n+1-x), nel disco De
(x) non cade alcun punto di S1, quindi xÏ
1; sia ora x Ï S1, allora x è compreso tra due numeri interi consecutivi: n < x < n+1, posto e = min(x-n; n+1-x), nel disco De
(x) non cade alcun punto di S1, quindi xÏ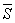 1, si conclude che
1, si conclude che 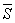 1 = S1.
1 = S1.
Vogliamo dimostrare che Q è denso in R, cioè che la sua chiusura è tutto R.
Occorre dimostrare che " x Î R e " intorno U di x, U contiene punti di Q.
Possiamo considerare un generico intorno di x della forma (x-e , x+e ). Sappiamo che tra due numeri reali distinti esiste almeno un numero razionale.
Determiniamo 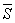 3, sappiamo che S3 è contenuto in
3, sappiamo che S3 è contenuto in 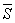 3, inoltre è facile vedere che 0 è di accumulazione per S4, d'altra parte si vede subito che se x < 0 oppure x > 1, x non può essere di accumulazione per S3. Si conclude che
3, inoltre è facile vedere che 0 è di accumulazione per S4, d'altra parte si vede subito che se x < 0 oppure x > 1, x non può essere di accumulazione per S3. Si conclude che 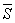 3 = [0,1].
3 = [0,1].
Possiamo ora determinare i derivati di S1, S2, S3. Le informazioni occorrenti per tale determinazione si desumono senza difficoltà da quanto visto sopra a proposito delle chiusure. Così si ha:
D(Z) = Æ , D(Q) = R, D(S3) = [0,1].
Risoluzione dell'Esercizio 2
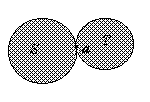
vediamo che SÇT = Æ , la cui chiusura è il Æ stesso,
mentre ![]() , quindi abbiamo che
, quindi abbiamo che
Æ = ![]() = {a}.
= {a}.
Risoluzione dell'Esercizio 3
Consideriamo R con la topologia euclidea:
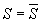
perché S è unione finita di chiusi.
D(S)=Æ
infatti sia S = { a1, …, an} con a1<…<an; sia e <min{|ai - ai -1|, |ai+1 - ai|}, l'intorno
(ai - e , ai + e ) non contiene altri elementi di S.
Consideriamo ora R con la topologia cofinita:
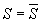
perché S è un chiuso.
D(S)=Æ
infatti R \ {a1, …, ai-1, ai+1, …, an} è un aperto che contiene ai, ma non contiene altri elementi di S.
Risoluzione dell'Esercizio 4
La chiusura di {a} è X, il derivato di {a} è X;
la chiusura di {e} è {e}, il derivato di {e} è Æ ;
la chiusura di {d, e} è {c, d, e}, il derivato di {d, e} è {c};
la chiusura di {a, c} è X, il derivato di {a, c} è {b, c, d, e};
la chiusura di {a, b} è X, il derivato di {a, b} è {b, c, d, e};
la chiusura di {a, d, e} è X, il derivato di {a, d, e} è {b, c, d, e}.
Risoluzione dell'Esercizio 5
Un tale spazio topologico esiste, infatti basta prendere un qualsiasi insieme X e dotarlo della topologia discreta.
Risoluzione dell'Esercizio 6