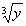Verifichiamo se f è continua:

f - 1 ({1}) = {a},

f ^{- 1} ({2,3}) = { b, c}, quindi f è continua.

Verifichiamo se f ^{- 1} è continua:

f({a}) = {1},

f({b, c)} = {1,2}, quindi f ^{- 1} è continua.

E' immediato vedere che f è biunivoca.

Verifichiamo che f è biunivoca:

per essere suriettiva deve valere " y Î R $ x Î R tale che f(x) = y, questo x è ;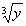

per essere iniettiva deve valere " x, y Î R, x ¹ y Þ f(x) ¹ f(y), ma è evidente che x³¹ y³.

Dimostriamo la continuità di f usando la continuità in ogni punto di R. Consideriamo x Î R. Per ogni e >0 esite d >0 tali che:

se y Î (x- d , x + d ) (intorno di x), allora f(y)= y³ Î (f(x) - e , f(x) + e ) = (x³ - e , x³ + e). Prendiamo ad esempio d = . Analogamente si dimostra che f ^-1 è continua.

g non è aperta, infatti g((-1, 1)) = [0,1).

Diamo un esempio di applicazione sia aperta che chiusa, ma non continua:

sia X = {1,2,3} sia t la topologia banale su X e t' la topologia discreta su X;

sia inoltre f: (X, t) ® (X, t') tale che f(1) = 3, f(2) = 2, f(3) = 1; i soli aperti del dominio sono Æ e X che sono anche i chiusi di (X, t ), quindi l'immagine di ogni aperto di (X, t ) è un aperto in (X, t'), stessa cosa per ogni chiuso;

ora consideriamo un aperto di (X, t'), per esempio {1},
f - 1 ({1}) = {3} che non è aperto di (X, t).

Consideriamo la funzione f: S¹ \ {p} ® R definita come in figura:

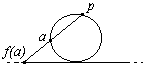
E' semplice dimostrare che si tratta di un omeomorfismo tra S¹ \ {p} ed R.

Sia (a, b) un qualunque intervallo di R.
Si puņ dimostrare che l'applicazione seguente č un omeomorfismo f: (a, b) ® R:

f(x) = 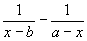.