Se S è un sottoinsieme di Q, contenente almeno due punti distinti p, q allora S è sconnesso. Infatti sia ad esempio p<q, $ e Î R \ Q con p<e <q Þ

U = (- ¥, e) Ç S e V = (e, +¥) Ç S sono aperti di S, disgiunti, non vuoti la cui unione è S.

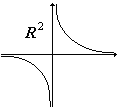
Osserviamo che H è omeomorfo ad R \ { 0}.
R \ {0} è costituito da due componenti connesse (- ¥ , 0) e (0, +¥ ). Quindi anche H ha due componenti connesse e precisamente le immagini attraverso l'omeomorfismo di R\{0} :
H₁ = HÇ{(x, y)ÎR²; x>0},
H₂ = HÇ{(x, y)ÎR²; x<0}.

X \ {(0,0)} ha due componenti connesse omeomorfe ad R mentre per ogni x Î I, I \ {x} è connesso oppure ha due componenti connesse ognuna omeomorfa ad un intervallo aperto da una parte e chiuso dall'altra e quindi non ad R.