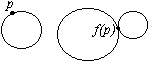
Risoluzione dell'Esercizio 1
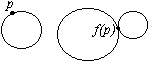
Supponiamo per assurdo che esiste un omeomorfismo f: X ® Y e sia p Î X il punto che ha come immagine il punto di tangenza delle due circonferenze.
Allora f|X\{ p} : X \ {p} ® Y \ {f(p)} è ancora un omeomorfismo.
Ma è un assurdo perché X \ {p} è connesso, mentre Y \ {f(p)} è sconnesso.
Risoluzione dell'Esercizio 2
![]() Supponiamo per assurdo che esista f: (a, b] ® (c, d) omeomorfismo.
Supponiamo per assurdo che esista f: (a, b] ® (c, d) omeomorfismo.
Sia p Î R tale che c<p<d il punto immagine di b.
Allora f|(a, b]\{ b} : (a, b] ® (c, d) \ {f(b)} è ancora un omeomorfismo. Ma (a, b] \ {b} è connesso mentre (c, d) \ {p} non lo è!
Risoluzione dell'Esercizio 3
{
(0, y) Î R2} È { (1, y) Î R2}{
(x, y) Î R2; x2 + y2 = 1} È {(x, y) Î R2; (x-2)2 + y2 = 1}che è un insieme connesso.
Risoluzione dell'Esercizio 4
Basta osservare che un qualunque punto di Y non lo sconnette, mentre esiste un punto che sconnette Z.
Risoluzione dell'Esercizio 5
Assumiamo per assurdo che esiste un omeomorfismo f: X ® S1. Sia x Î S1 tale che f((0,0)) = x, allora la restrizione f| X \ {(0,0)} : X \ {(0,0)} ® S1 \ {x} è ancora un omeomorfismo, ma X \ {(0,0)} è sconnesso, mentre S1 \ {x} è connesso.