In questo ipertesto è introdotta una disciplina relativamente "nuova" della matematica, le cui origini possono essere rintracciate dalla metà del '700: la Topologia. Essa è lo studio di quegli insiemi in cui viene considerata la nozione di "prossimità"... abbastanza per decidere se una funzione definita su di essi è continua. Si tratta di un tipo di geometria generalizzata. Si interessa comunque di sfere e cubi (per esempio), ma in essa vengono considerati "oggetti uguali". Infatti possiamo prendere uno di essi e trasformalo nell'altro stirandolo o schiacciandolo senza però lacerarlo.

Sappiamo che ciò che distingue i differenti rami della geometria è il tipo di trasformazioni che occorre applicare ad un oggetto perché questo sia effettivamente cambiato. In Topologia è lecita ogni trasformazione continua. Dove per "continua" si intende che punti "vicini" prima della trasformazione, restano tali anche dopo. Ad esempio un cerchio ed una figura 8 non sono topologicamente lo stesso oggetto, infatti possiamo schiacciare al centro un cerchio ed ottenere l'8, ma non possiamo effettuare il procedimento contrario senza essere costretti a spezzare il collegamento al centro. In questo modo punti che prima si trovavano vicino al punto centrale di connessione, poi si troveranno nei lati opposti del cerchio. Dato che gli assiomi della Topologia sono assegnati in termini di sottoinsiemi di un insieme generico X, essa è strettamente collegata alla teoria degli insiemi.

Il primo lavoro che si può considerare come l'introduzione della Topologia è dovuto ad Eulero. Egli pubblicò nel 1736 uno scritto sulla soluzione del Problema dei ponti di Königsberg intitolato Soluzione di un problema concernente la geometria della posizione. Il titolo in sé indica che Eulero era consapevole che si stava addentrando in un tipo differente di geometria in cui il concetto di distanza diveniva irrilevante.

Il documento non indicava soltanto che attraversare i sette ponti della cittá (vedi figura) in un singolo viaggio era impossibile, ma generalizzava, mostrando che (in notazione moderna): in un grafo, è possibile percorrere tutti i bordi esattamente una volta se e solo se in esso due vertici hanno grado dispari. Nasceva, così, una concezione nuova della geometria che si liberava di tutte le concezioni metriche e "rigide" accumulate in millenni di storia del pensiero.

Lo studio della Topologia, da allora, si è sviluppato enormemente passando da Riemann nell'800 fino a Poincaré agli inizi del nostro secolo, ed ha mostrato quanti e quali oggetti "impossibili" sia possibile concepire. La costruzione di nuovi oggetti topologici è soggetta a meno vincoli di quelli euclidei. La scoperta di oggetti topologicamente nuovi ha permesso di introdurre in questo mondo oggetti che di questo mondo non hanno certo l'aspetto.

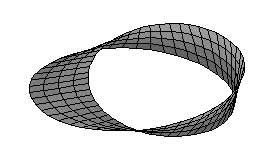Un esempio elementare è quello del nastro di Moebius. Si tratta di un oggetto particolare che ha un solo bordo ed una sola faccia, cioè non ha superfice interna ed esterna, come per esempio un cilindro. Per questo il nastro di Moebius si distingue dal cilindro proprio per le sue proprietà topologiche.

La pervasività della Topologia nella scienza moderna è impressionante: la Fisica, a tutti i livelli, dalla Teoria delle Particelle Elementari alla Cosmologia, ne fa un uso massiccio.

Una caratteristica degli oggetti nella Topologia è che possono essere concepiti in modo intrinseco, cioè non immersi in uno spazio ulteriore, come accadeva in genere per gli oggetti della Geometria Euclidea. Anzi, lo spazio stesso diviene un oggetto geometrico, suscettibile di studio nella sua totalità. In questo ipertesto trattiamo gli assiomi di base della Topologia, introducendo la definizione di spazio topologico, di intorno, il concetto di insieme aperto e/o chiuso, le trasformazioni continue ecc. Vedremo inoltre una delle proprietà invarianti per trasformazioni continue: la connessione.