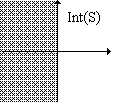Esempio 1

Consideriamo in (R², e) l'insieme S = {(x, y) | x£0}; allora
Int(S)={(x, y) | x<0}
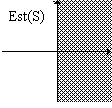
Est(S)={(x, y) | x>0}
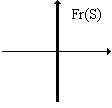
Fr(S)={(x, y) | x=0}

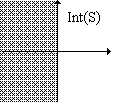Esempio 2 Sia R con la topologia euclidea, consideriamo l'insieme S = { | nÎN, n¹0}; allora
Int(S)=Æ;
Est(S)=R \ (SÈ{0});
Fr(S)=(SÈ{0}).

Sia R con la topologia cofinita:
Int(S)=Æ;
Est(S)=Æ;
Fr(S)=R.

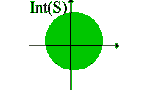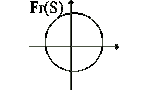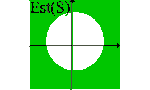
Esempio 3

Consideriamo in (R², e) l'insieme S = {(x, y) | x²+y²£1}; allora
Int(S)={(x, y) | x²+y²<1}
Est(S)={(x, y) | x²+y²>1}
Fr(S)={(x, y) | x²+y²=1}

Esempio 4

Sia R² con la topologia euclidea, consideriamo l'insieme S=D₁((0,0))È{(2,0)}; allora:
Int(S)=D₁((0,0));
Est(S)=R² \ ({(x, y) | x²+y²£1}È{(2,0){);
Fr(S)={(x, y) | x²+y²=1}È{(2,0)}

Esempio 5

La frotiera di S puņ appartenere o no ad S, infatti nell'esempio2 qui sopra: Fr(S)ËS; mentre nell'esempio1 Fr(S)ÍS.

Esempio 6

X=Int(S)ÈEst(S)ÈFr(S), questa situazione è ben evidente negli esempi1 e 3 sopra.

Esempio 7

Consideriamo l'aperto di R², D₁((0,0)), allora:
Int(S)=D₁((0,0));
Est(S)={(x, y) | x²+y²=1};
Fr(S)={(x, y) | x²+y²=1} evidentemente Fr(S)ÇS=Æ.

Esempio 8

Sia X={1,2,3,4} con la topologia t={Æ, X, {1}, {2}, {1,2}, {2,3}, {1,2,3}}, siano
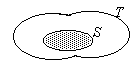
S={2,3} e T={1,2,3} sottoinsiemi di X con SÍT; Int(S)=Æ e Int(T)={1,2,3}=T, ovviamente si ha che ÆÍT;
Siano ora S={1,2} e T={2,3,4}, allora SÇT={2} abbiamo che Int(SÇT)={2};
Int(S)={1,2}=S ed Int(T)={2,3}, allora Int(S)ÇInt(T)={2};
Ora Int(S)ÈInt(T)={1,2,3}, SÈT={1,2,3,4}, quindi Int(SÈT)=X, notiamo che {1,2,3} è strettamente contenuto in X.

Esempio 9

Se SÍT, allora Int(S)ÍInt(T)	Int(SÇT)	Int(SÈT)

Esempio 10