Esempi sugli intorni di un punto e le basi di intorni
Consideriamo R2 con la topologia euclidea. L'insieme A, in figura, è un aperto e l'insieme U è un intorno del punto x.
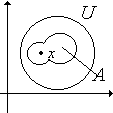
Esempio
2
Consideriamo X insieme non vuoto con la topologia banale; allora per ogni punto x di X, l'unico intorno di x
è X stesso.
Esempio
3
Consideriamo X insieme non vuoto con la topologia discreta; allora per ogni
punto x di X,
{x
}
è un intorno di x come lo
è qualsiasi sottoinsieme di X che
contenga x.
Esempio
4
Sia X uno
spazio topologico; la famiglia di tutti gli intorni di x è una base di intorni per x.
Esempio
5
Sia (R, e
), sia d
Î R, la famiglia degli
intervalli aperti (x - d, x + d)
è una base di intorni di x.
Esempio
6
R2
con la topologia euclidea soddisfa il primo assioma di numerabilità.
In generale Rn
soddisfa il primo assioma di numerabilità.
Questo lo vediamo negli esempi della prossima parte.
Esempio
7
Ogni spazio discreto soddisfa il primo assioma di
numerabilità, perché per ogni x
Î X, {{x}} è
una base di intorni di x.