Esempi sulle funzioni continue

 

 

Esempio 1

 

id: (X, t) ® (X, t) è continua.

 

In generale non è vero che id : (X, t) ® (X, t') sia continua se t ¹ t'.

Anzi si può dire che è continua se e solo se t' < t.

 

 

 

Esempio 2

 

Siano X e Y spazi topologici e sia f: X® Y un'applicazione costante (cioè f(X) = a Î Y) è continua.

 

 

 

Esempio 3

 

Ogni applicazione di uno spazio discreto X in uno spazio qualsiasi Y è continua;

ogni applicazione di uno spazio qualsiasi X in uno spazio banale Y è continua.

 

 

 

Esempio 4

 

Consideriamo R ⁿ e R con la topologia euclidea. Una funzione polinomiale f : R ⁿ® R tale che f(x₁, …, x_n) = a₁x+ …+a_nxⁿ   è continua. Vediamo un caso particolare:

f :R³® R tale che f(x, y, z) = 2xy² - z³ + xz⁴ è un'applicazione continua.

 

In particolare sono continue le proiezioni p_i : R ⁿ® R tali che p_i(x₁,   , x_n) = x_i.

 

Osserviamo che un’applicazione f: R³ ® R^m è continua se e solo se le sue componenti f_j : R³ ® R con j=1,…,m, sono continue.

 

 

 

Esempio 5

 

Consideriamo il sistema:

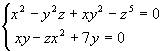
non sappiamo se ha soluzioni, ma siamo certi che l'insieme C delle sue soluzioni è un chiuso in (R³, e).

Infatti definiamo f : R ³® R²  tale che f(x, y, z) = (x² - y²z + xy² - z⁵, xy - zx² + 7y); per quanto osservato nell’esempio precedente, f risulta continua.

Quindi C = f^--1((0, 0)) è chiuso perché {(0, 0)} è chiuso in R².

 

 

Esempio 6

 

L'insieme C definito come nell'esempio 5 qui sopra, è una esempio di fibra di f.

Più in generale  questo è vero per l'insieme delle soluzioni di un qualsiasi sistema di equazioni.

 

 

 

Esempio 7

 

p: R²®R tale che p(x, y) = x è aperta, ma non chiusa, infatti "essere aperta" e "essere chiusa" sono proprietà indipendenti l'una dall'altra. Sia

C = {(x, y)| xy - 1=0}

 allora p(C) = R \ {0} che non è un chiuso in R, mentre C lo è.

 

 

Esempio 8

 

Vediamo un esempio di applicazione chiusa, ma non aperta: sia C chiuso in uno spazio topologico X, sia i: C® X  l'inclusione di C in X; essa è ovviamente chiusa, ma non è aperta, infatti usiamo la

Proposizione: S aperto in X Û i: S® X aperta;

         S chiuso in X Û i: S® X chiusa.

la cui dimostrazione è data per esercizio.

 

 

Esempio 9

 

(R², e);  r = {(x, y)| x - y + 5= 0},

i: r®R² è chiusa, ma non aperta.

(Vedere esempio8).