Esempi sulla Connessione per Archi

 

 

Esempio 1

 

Rⁿ è connesso per archi perché " a, b Î Rⁿ il segmento che li congiunge è un arco.

Vediamo R²:

 

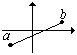
Esempio 2

 

D₁((0,0)) Í R² è connesso per archi:

 

 

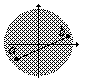
Esempio 3

 

I ⁿ è connesso per archi.

Vediamo I ²:

 

 

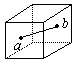
Esempio 4

 

Consiederiamo l'insieme X = A È B come in figura. X non è connesso per archi, infatti A e B sconnettono l'arco a(I).

 

 

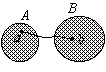
Esempio 5

                            

 

In R² se il sottoinsieme non è convesso, non è possibile usare il segmento come arco; occorre trovare un punto al centro in modo da costruire l'arco come in figura.

 

 

Esempio 6

 

S¹ è connessa per archi, infatti siano:

f: [0,1] ® S¹ ove f(t) = (cos2pt, sen2pt); f_{½[q, j]} : [q, j] ® S¹ e sia  g: [0,1] ® [q, j] omeomorfismo, allora definiamo l'arco: a = fg.

 

 

 

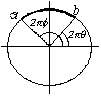
Esempio 7

 

S ⁿ è connesso per archi. Vediamo il caso S ²:

p piano per 0 e a, p Ç S ² » S¹;

p' piano per 0 e b, p' Ç S ² » S¹;

vediamo che le due circonferenze intersecandosi formano un arco che unisce a e b.

 

 

 

Esempio 8

 

Vediamo un esempio di insieme connesso ma non connesso per archi:

sia C = {(1/n, y) | 0 £ y £ 1 e n ³ 1} e l'intervallo unitario dell'asse x

I_x = {(x, 0) | 0 £ x £ 1}

vediamo che l'insieme I_x È C è connesso per archi, quindi connesso. Consideriamo ora il punto p = (0,1), l'insieme

X = I_x È C È {p}

 

è connesso perché p appartiene alla chiusura di I_x È C (in particolare appartiene al suo derivato). D'altra parte X non è connesso per archi. Per mostrare questo è sufficiente far vedere che se a : [0,1] ® X è un arco tale che a(0) = p allora " t Î [0,1], a(t) = p. In altri termini, ogni arco che ha come punto iniziale p resta tutto contenuto in p stesso.

Sia

G = a ^-1(p) Í [0,1];

G è chiuso perché a è continua. Sia t Î G e D = D_1/2 (p), per la continuità di a, esisted > 0 tale che

a((t - d, t + d)) Í D Ç X.

Ma a((t - d, t + d)) è un connesso che contiene p, quindi coincide con p, perché ogni sottoinsieme di DÇX contenente p è sconnesso se contiene altri punti. Quindi

(t - d, t + d) Í G

ne segue che G è aperto e chiuso in [0,1] Þ G = [0,1], perché [0,1] è connesso.

 

 

 

Esempio 9

 

L'immagine continua di un connesso per archi è connessa per archi; ad esempio:

sia f: [0,1] ® S¹, ove f(t) = (cos2pt, sen2pt);
f è continua e suriettiva, allora S¹ è connessa per archi.

 

 

 

 

Esempio 10

 

X = AÈ B, A e B sono le due componenti connesse per archi di X.

 

 

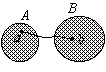
Esempio 11

 

Nell'esempio8, l'unica componente connessa per archi di X che contiene il punto p è {p}.