Esempi sulla Connessione

 

 

Esempio 1

 

Un qualsiasi insieme X con la topologia banale è connesso;

X con almeno due punti dotato di topologia discreta non è connesso, infatti se x Î X, allora X = {x}È(X \{x});

X con la topologia cofinita è connesso se e solo se è infinito, oppure se è costituito da un solo punto.

R con la topologia cofinita è connesso.

 

 

 

Esempio 2

 

Rⁿ (n ³ 1) con la topologia euclidea è connesso.

 

 

 

Esempio 3

 

Sia p un punto di (Rⁿ, e), l'insieme Rⁿ \ {p} è connesso se e solo se n > 1.

 

Questo implica che R \ {p} è sconnesso (diciamo anche che p sconnette R).

 

 

 

Esempio 4

 

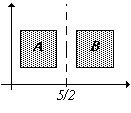
Consideriamo gli insiemi A e B come in figura. Siano H₁ = {(x, y) | x < 5/2} e H₂ = {(x, y) | x > 5/2} due aperti di R².

Consideriamo l'insieme X Í R², con la topologia indotta da e di R², definito in questo modo:

X = A È B .

X è tale che:
XÇH₁ = A e

XÇH₂ = B;

A e B sono aperti di X e sono tali che AÇB = Æ, quindi X è sconnesso.

 

Esempio 5

 

X = [0,1] è connesso (vedi Teorema1.5);

mentre X = [0,1] \ {1/2} è sconnesso, infatti X = ((-¥, 1/2) Ç X) È ((-1/2, +¥) Ç X).

 

 

 

 

Esempio 6

 

Sia f: [0,1] ® S¹, ove f(t) = (cos2pt, sen2pt); f è continua e suriettiva ([0,1] è connesso), quindi, per la proposizione 1.7, S¹ è connessa;

Se consideriamo X = f((1/2, 1]), per la stessa ragione, è connesso:

 

 

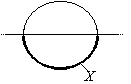
Esempio 7

 

Uno sconnesso può avere un'immagine attraverso una applicazione continua che sia connessa:

X = {y = 1}È{y = 2}, sia p: R² ® R ove p((x, y)) = x; allora p| X: X ® R è continua e suriettiva, ma R è connesso e X è sconnesso.

 

 

 

 

Esempio 8

 

Sappiamo che R » S¹ \ {p} dove p è un punto di S¹; essendo R connesso, allora S¹ \{p} è connesso.