
Dimostrazione
BÇJ
¹
Æ, (AÇJ)
Ç
(BÇJ)=Æ
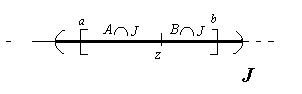
J intervallo Þ [a, b]
Í J; AÇ[a, b] è chiuso.
Essendo A Ç [a, b]
¹ Æ, $ z = sup(AÇ[a, b]) e
certamente a £ z £ b. Proviamo che z Î AÇB e così si avrà l'assurdo:
essendo
A Ç [a, b] chiuso, dalla definizione di sup segue che z
Î AÇ[a, b]; z è aderente ad AÇ[a, b]
e quindi z Î AÇ[a, b] Þ z Î A;
se
z = b allora z Î B siamo a posto,
se
z < b allora (s, b] Í B (altrimenti $ c Î (z, b] tale che c Ï B
quindi c Î A cioè c Î AÇ[a, b] e c > z
che contraddice il fatto che z sia il sup), quindi z è aderente a
B che è chiuso Þ z Î B.
Viceversa
se Y Í R è connesso, allora Y è un
intervallo,
infatti
se non lo fosse $ a, b, c Î R tali che a < b < c e a, c Î Y e b Ï Y, ma allora Y=((-¥, b)ÇY)È((b, +¥)ÇY) cioè Y non sarebbe connesso.