Esame di Geometria II - 13.9.00
I appello sessione autunnale - a. a. 1999/2000
In R2 è dato il sottoinsieme
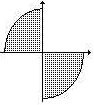
Y = { (x, y) Î R2 | xy<0 e x2+y2£1}
Soluzione

(R2, e): Int(Y) = { (x, y) Î R2 | xy<0 e x2+y2 < 1}; Est(Y) = R2 \ Y; Fr(Y) = { (x, y) Î R2 | xy<0 e x2+y2 = 1} |
(R2, topologia discreta):
Int(Y) = Y; Est(Y) = R2 \ Y; Fr(Y) = Æ; |
(R2, topologia cofinita):
Int(Y) = Æ; Est(Y) = Æ; Fr(Y) = R2. |
Y è unione di due aperti disgiunti nella topologia indotta da e di R2.