Esame di Geometria II - ottobre 95

II appello sessione autunnale - a. a. 1994/95

 

 

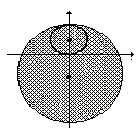
Si consideri il seguente sottoinsieme X di R2 con la topologia euclidea:

X = { (x, y) Î R2 | x2+(y-1)2 =1} È { (x, y) Î R2 | x2+(y+2)2 £ 4}

  1. Si determinino Int(X), Est(X), Fr(X).

  2. X è connesso per archi?

Soluzione

  1. Int(X) = {(x, y) Î R2 | x2+(y+2)2 < 4}

    2. Est(X) = {(x, y) Î R2 | x2+(y+2)2 >4}

    Fr(X) = {(x, y) Î R2 | x2+(y+2)2 = 4}

  2. X è un disco chiuso di centro (0, -2) e raggio 4; X è connesso per archi perché per ogni coppia di punti in X, il segmento che li congiunge è contenuto in X.