Superfici in coordinate cilindriche
Un metodo che consente di determinare
l’equazione di una superficie di rotazione rispetto all’asse 
(o rispetto ad un qualsiasi asse
cartesiano) , consiste nell’applicare le proprietà delle coordinate
cilindriche (1). Si applica quando la curva giace in un piano
coordinato.
Se si considera nello spazio un sistema di
coordinate cilindriche 
, poiché ogni parallelo di 
ha una equazione del tipo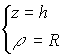 
, allora una superficie di rotazione di asse avrà equazione 
(ogni parallelo ha un
raggio che dipende dalla quota), con 
. In generale il metodo ci consente
di passare dall’equazione di una curva 
definita (in coordinate cartesiane) dal sistema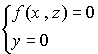 
, all’equazione
della superficie in coordinate
cilindriche, sostituendo semplicemente la variabile 
al posto di 
nella prima delle due equazioni del sistema.
Riprendendo l’esempio visto
nell’introduzione e applicando il metodo alla curva di equazione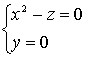 
, otteniamo 
, con 
arbitrario, da cui essendo 
, si ha 
.
In generale, per una superficie del tipo 
, intersecando
la con
piani ortogonali all’asse di rotazione, si può ottenere un numero di circonferenze
maggiore di uno.
Consideriamo come esempio la curva di equazione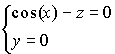 
,
dall’applicazione del metodo otteniamo la superficie di rotazione di asse di equazione 
, ossia 
.
Se si interseca questa superficie con un
qualsiasi piano 
di
equazione 
con 
otteniamo infinite
circonferenze di centro 
, in particolare scelto 
, otteniamo infinite circonferenze di raggio 
con 
come illustrato in figura.