Gli esempi visti in precedenza, costituivano casi particolari di superfici di rotazione. Nel caso più generale, possiamo generare una superficie facendo ruotare una qualsiasi curva piana attorno ad un asse scelto in modo arbitrario.

Se   ha  equazioni parametriche, , ,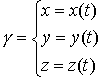

ed equazioni cartesiane

,

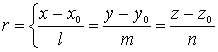allora il parallelo di centro con dove è il piano ad passante per il punto  ,  è descritto da un sistema di due equazioni, di cui la prima rappresenta l’equazione della sfera di centro e raggio , mentre la seconda rappresenta l’equazione del piano .

figura 2.1 (puoi interagire con l'oggetto)

Per determinare l’equazione cartesiana della superficie, si dovrà successivamente eliminare il parametro presente tra le due equazioni.

Determinare la superficie di rotazione ottenuta facendo ruotare attorno all’asse di equazioni 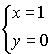,  la retta passante per i punti

e .

Soluzione

Una parametrizzazione della retta per e è 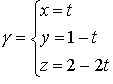, mentre il piano normale a ha equazione . Sostituendo quest'ultima equazione nella parametrizzazione di si ottiene l’espressione in del punto , cioè , mentre per otteniamo .
L’equazione del parallelo di centro passante per e di raggio sarà allora 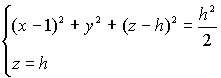, eliminando il parametro  dal sistema si

ottiene l’equazione cartesiana .