Definizioni
Una superficie ![]() si definisce superficie di rotazione di asse
si definisce superficie di rotazione di asse
![]() se
se ![]() e’ costituita da circonferenze aventi il centro su
e’ costituita da circonferenze aventi il centro su ![]() e giacenti su piani ortogonali ad
e giacenti su piani ortogonali ad ![]() .
.
Se ![]() è una curva nello
spazio, la sua rotazione attorno ad un asse
è una curva nello
spazio, la sua rotazione attorno ad un asse ![]() descriverà una superficie rotonda
descriverà una superficie rotonda ![]() , di cui
, di cui ![]() è l’asse di rotazione. Ogni punto
è l’asse di rotazione. Ogni punto![]() descrive una
circonferenza detta parallelo della superficie di rotazione,
in un piano ortogonale a
descrive una
circonferenza detta parallelo della superficie di rotazione,
in un piano ortogonale a ![]() ,
mentre ogni piano contenente la retta
,
mentre ogni piano contenente la retta ![]() interseca la superficie
interseca la superficie ![]() in
una curva meridiana. Ciascun meridiano è una curva
simmetrica rispetto all’asse di rotazione, ed incontra ogni parallelo in due punti
simmetrici rispetto all’asse.
in
una curva meridiana. Ciascun meridiano è una curva
simmetrica rispetto all’asse di rotazione, ed incontra ogni parallelo in due punti
simmetrici rispetto all’asse.
Esempio 1:
Il paraboloide di equazione : ![]() è una superficie di
rotazione ottenuta facendo ruotare la parabola di equazione
è una superficie di
rotazione ottenuta facendo ruotare la parabola di equazione 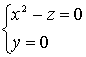
attorno all’asse ![]() .
.