Esempio di cuspide
 ove
ove continua
continua  xÎ
xÎ Poichè
Poichè  essa è derivabile
essa è derivabile  xÎ
xÎ -{1}
Osservando che si ha
-{1}
Osservando che si ha e che
e che
 f '(x) = +
f '(x) = +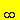 e
e  f '(x) = -
f '(x) = -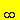 si ottiene:
si ottiene: Si deduce che x = 1 è un punto di minimo relativo per la funzione.
Essendo poi
Si deduce che x = 1 è un punto di minimo relativo per la funzione.
Essendo poi  f '(x) = ±
f '(x) = ±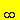 la curva ha nel punto B(1,0) una sola retta tangente parallela
all'asse y, di equazione x = 1
Il punto B si dice cuspide con vertice in basso
la curva ha nel punto B(1,0) una sola retta tangente parallela
all'asse y, di equazione x = 1
Il punto B si dice cuspide con vertice in basso