Esempi sulla ricerca di massimi e minimi
Determinare nell'intervallo [0,5] il massimo e il minimo assoluto della funzione:
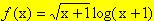. Calcoliamo dunque la derivata prima:
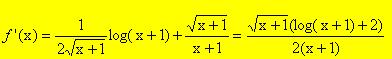
log(x+1)+2 >0 in ]-1,+
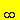[Notiamo che la funzione è derivabile in tutto l'intervallo [0,5].
Deduciamo che il massimo e il minimo assoluto si trovano negli estremi percio' calcoliamo f(0) = 0 e f(5) =
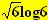
Il minimo assoluto è 0, nel punto di ascissa 0, e il massimo assoluto è
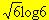, nel punto di ascissa 5, in accordo col fatto che la derivata
è positiva in [0,5].
Se una funzione f non è derivabile in qualche punto del dominio, per determinare i suoi massimi e minimi eventuali occorre confrontare i massimi e i minimi ottenuti nei punti di derivabilità con i valori della funzione nei punti dove essa non è derivabile.
Ad esempio, ricerchiamo i massimi e i minimi della funzione
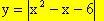Essa è definita a tratti: 
Il suo grafico è il seguente
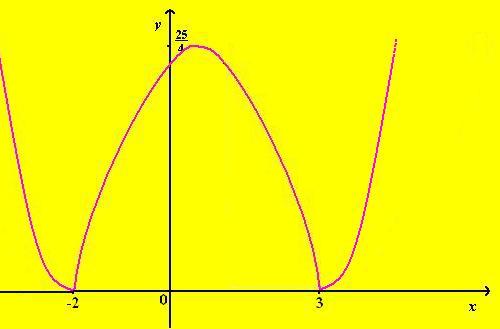
Calcolando la derivata prima otteniamo: 2x-1 se x <-2
-2x+1 se -2
x 32x-1 se x >3
Tale derivata consente di trovare l'unico massimo relativo in x =1/2
I punti in cui f non è derivabile sono dunque due punti di minimo.