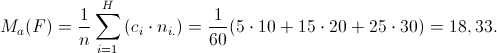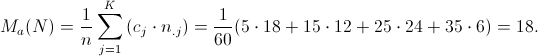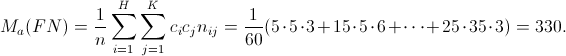ESERCIZIO 2
In un supermercato, durante l'arco di un quadrimestre, sono stati monitorati gli acquisti dei pacchi di acqua frizzante (F) e naturale (N) mediante l'utilizzo di 60 carte fedeltà.
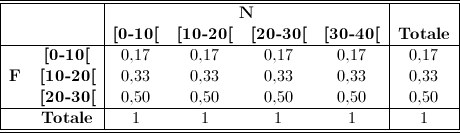
Di seguito è riportata la tabella a doppia entrata costruita con i dati ottenuti.

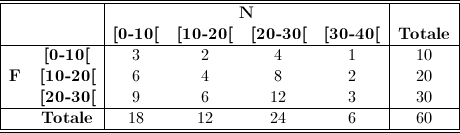
1. Formulare statisticamente la situazione considerata individuando: il collettivo in esame, la sua numerosità, la singola unità statistica, i caratteri considerati e la loro tipologia.
Soluzione del punto 1:
U: Collettivo composto dalle 60 carte fedeltà monitorate; ogni carta fedeltà rappresenta la singola unità statistica.
La numerosità del collettivo è n=60.
I caratteri considerati sono: F=Numero di pacchi d'acqua frizzante acquistati con una particolare carta fedeltà; N=Numero di pacchi d'acqua naturale acquistati con una particolare carta fedeltà.
I due caratteri sono di tipo quantitativo discreto e come si può notare sono stati suddivisi in classi disgiunte e della stessa ampiezza.
Soluzione del punto 2:
Il carattere F si dice statisticamente indipendente da N se, qualunque sia la modalità con cui si manifesta il carattere N, la distribuzione relativa condizionata di F rimane sempre la stessa, cioè i profili colonna della tabella a doppia entrata sono tutti uguali fra loro. Calcoliamo dunque i profili colonna della tabella a doppia entrata:
I profili colonna risultano essere tutti uguali fra loro. Si può dunque affermare che i due caratteri considerati sono statisticamente indipendenti.
Si osservi inoltre che un'ulteriore conferma viene data dal calcolo delle frequenze teoriche di indipendenza, definite da
che nel caso di indipendenza statistica devono coincidere con quelle empiriche
.
Per esempio si ha infatti:e lo stesso si può facilmente verificare per tutte le rimanenti frequenze teoriche di indipendenza.
Soluzione del punto 3:
Si definisce baricentro la coppia
data dalle medie aritmetiche dei due caratteri.
Grazie alla tabella a doppia entrata, conosciamo la distribuzione di frequenze dei due caratteri (distribuzioni marginali della tabella a doppia entrata). Inoltre, considerando che i due caratteri sono stati suddivisi in classi del tipo
, sarà necessario approssimare le medie aritmetiche utilizzando il valore centrale di ogni classe, dato da
Per calcolare le due medie aritmetiche utilizziamo quindi le seguenti formule:
Il baricentro risulta quindi uguale a (18,33;18).
Soluzione del punto 4:
Avendo già i valori delle due medie aritmetiche dal punto 3., per calcolare la covarianza tra F e N possiamo usare la formula:
A partire dalla tabella a doppia entrata calcoliamo dunque:
Da cui risulta:
Si osserva che questo risultato è in accordo con la proposizione che dice che se due caratteri sono statisticamente indipendenti allora la loro covarianza è nulla.
Chiaramente il valore 0,06 è dovuto a tutte le approssimazioni compiute fino a questo punto; se avessimo tenuto tutti i risultati sotto forma di frazioni avremmo certamente ottenuto zero, senza necessità di arrotondare.
NB: Si ricordi però che non vale l'implicazione opposta!
Soluzione del punto 5:
Il coefficiente di correlazione lineare di Bravais e Pearson è definito come:
Considerando che al punto 4. abbiamo trovato che la covarianza è nulla, in quanto i due caratteri sono statisticamente indipendenti, si ha che
In particolare si ricordi che il coefficiente di correlazione lineare è un indice relativo che assume valori nell'intervallo [-1,1], assumendo il valore degli estremi nel caso di perfetto legame lineare, che in questa situazione evidentemente non si verifica.
Soluzione del punto 6:
Per calcolare la retta di regressione N*=a*+b*F bisogna ottenere la coppia (a*, b*) data dalle seguenti formule:
Si ottiene quindi la retta di regressione N*=18 che è una retta orizzontale che interseca l'asse delle ordinate all'altezza del valore della media aritmetica del carattere N.
Si noti che il coefficiente di regressione b* è risultato nullo a causa della covarianza, nulla in quanto i due caratteri sono statisticamente indipendenti.
L'indipendenza statistica tra i due caratteri è dunque ulteriormente esplicata dal risultato ottenuto: la retta di regressione orizzontale comunica che il modello non è in grado di prevedere alcun tipo di variazione del carattere N in corrispondenza di una variazione del carattere F (al variare di F il valore di N previsto dalla retta di regressione rimane costante).
Soluzione del punto 7:
L'indice di determinazione è definito come quadrato del coefficiente di correlazione; risulta quindi
Si ricordi che la varianza totale può essere scritta come somma della varianza spiegata e della varianza residua e che l'indice di determinazione è una misura relativa della riduzione della variabilità di N, ottenuta proprio rapportando la varianza spiegata su quella totale.
Questo dato ci indica che la retta di regressione spiega lo 0% della variabilità totale, il che fa sì che in questo caso la varianza totale coincida con quella residua.
In conclusione si può dire che nel supermercato in questione non vi è correlazione tra l'acquisto dei pacchi di acqua frizzante e l'acquisto dei pacchi di acqua naturale, in quanto i due caratteri sono statisticamente indipendenti, e non è quindi possibile prevedere le variazioni degli acquisti dell'uno date le variazioni degli acquisti dell'altro.