3.1 Per calcolare la media condizionata di Y rispetto alla modalità =5 di X, utilizziamo la seguente formula, osservando che in questo caso i=3:

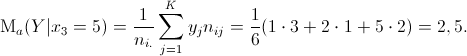
3.2 Il carattere X si dice statisticamente indipendente da Y se, qualunque sia la modalità con cui si manifesta il carattere Y, la distribuzione relativa condizionata di X rimane sempre la stessa, cioè i profili colonna della tabella a doppia entrata sono tutti uguali fra loro. Si dimostra poi che se X è indipendente da Y allora vale anche il viceversa.

Calcoliamo dunque i profili colonna della tabella a doppia entrata:

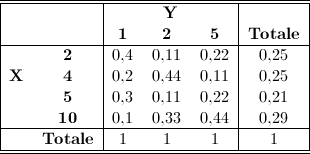
Evidentemente i profili colonna non sono tutti uguali fra loro. Si può dunque affermare che i due caratteri considerati non sono statisticamente indipendenti.

Si osservi inoltre che un'ulteriore conferma viene data dal calcolo delle frequenze teoriche di indipendenza, definite da che nel caso di indipendenza statistica devono coincidere con quelle empiriche . Per esempio si ha infatti:

Per calcolare la covarianza possiamo utilizzare la formula:

Utilizzando le distribuzioni marginali, calcoliamo dunque le medie aritmetiche necessarie:

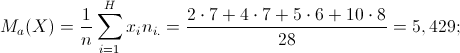
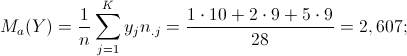
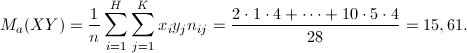
Si otterrà:

Calcoliamo quindi le deviazione standard dei due caratteri X e Y.

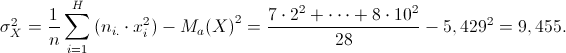
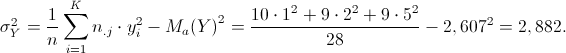
Da cui seguono:

In conclusione risulterà:

Questo risultato ci comunica che i due caratteri sono positivamente correlati.