- La stima della probabilità
-
- La matematica non è soltanto quel complesso di regole e operazioni che ci aiutano nella vita pratica di ogni giorno, e nemmeno soltanto un insieme astratto di concetti da imparare per non prendere un brutto voto a scuola. La matematica è anche un universo pieno di magia: sotto i più comuni ragionamenti matematici, che facciamo quotidianamente senza pensarci, si nascondono delle implicazioni sorprendenti.
- Ennio Peres
Spesso nella vita quotidiana affrontiamo scelte di cui non sappiamo prevedere le conseguenze. La parte della matematica che si occupa di razionalizzare le interpretazioni dei fenomeni casuali, invece che affidarsi a pregiudizi, a superstizioni o al fato, è detta calcolo delle probabilità.
Il calcolo delle probabilità è uno strumento essenziale per la statistica. Esso dà una risposta a quello che possiamo considerare come il problema inverso di quello della statistica inferenziale. Mentre la statistica cerca di determinare tramite la conoscenza dei risultati di un esperimento (o più esperimenti) quali siano le caratteristiche della popolazione su qui l'esperimento è stato eseguito, nel calcolo delle probabilità si assume che tutte le caratteristiche della popolazione siano note (senza preoccuparsi di come ciò sia possibile) e si vuole calcolare a priori la "probabilità" che un esperimento abbia un determinato risultato.
In matematica in particolare, ma anche in gran parte delle altre discipline, affrontare un problema comporta il saperlo vedere dal punto di vista migliore o il saperlo trasformare in un problema sostanzialmente equivalente ma che abbia forma o metta meglio in evidenza collegamenti a concetti e procedure o … che lo rendano più "concretamente" esplorabile alla nostra mente. Quesiti a cui si debba rispondere in poco tempo si prestano alla verifica di questa capacità, che purtroppo non sono molto curate dalle più diffuse pratiche di insegnamento/verifica, che (dalla scuola dell'obbligo fino all'università) privilegiano spesso una impostazione a "comportamenti stagni".- La possibilità di poter disporre di un apparato matematico per il calcolo delle probabilità, permette di superarne le insidie, che sono di varia natura, ma sono in buona parte legate a una eccessiva confidenza nelle capacità dell'intuizione. Ne esaminiamo alcune che appaiono come le principali fonti di errore nella valutazione della probabilità di eventi di interesse.
-
Il conteggio dei casi
Una prima fonte di errore è, nel caso di spazi finiti, il conteggio dei casi. Nell'esempio del lancio dei due dadi, confondere i due eventi: "uscita di (1,6)" e "uscita di un 1 e di un 6" porterebbe a conclusioni scorrette in quanto:
- 1/36 = P(uscita di (1,6))
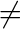 P( uscita di un 1 e di un 6) = P(uscita
(1,6)) + P(uscita(6,1))= 1/18.
P( uscita di un 1 e di un 6) = P(uscita
(1,6)) + P(uscita(6,1))= 1/18.
- Spesso i principianti sono messi in difficoltà di fronte alla richiesta di calcolare la probabilità di eventi di tipo "almeno", che è invece facilmente ottenibile considerando l'evento complementare.
- Ad esempio dall'identità P(Ā)=1-P(A), si ottiene immediatamente:
- P(almeno una faccia >2) = 1 - P(tutte e due le facce ≤ 2) = 1- P((1,1) U (1,2) U (2,1)) = 1 - 3/36
Per spazi campionari finiti, il calcolo delle probabilità richiede tipicamente l'utilizzo delle formule di calcolo combinatorio.
-
L'abuso dell'equiprobabilità
- Un'altra insidia è costituita dalla supposizione dell'equiprobabilità delle diverse alternative. Per esempio l'ipotesi che la distribuzione di probabilità del picco orario di chiamate ad un call center sia uniforme sulle 24 ore può essere certamente semplificatrice dal punto di vista del calcolo, ma ne appare evidente il limite (almeno che non si stia considerando un call center operante su scala mondiale).
- Occorre ricordare che un modello probabilistico, come ogni modello, costituisce comunque una approssimazione della realtà; ipotesi semplificatrici possono essere opportune per un primo approccio ad una situazione complessa. Spesso la semplificazione permette di ottenere risposte comunque utili, che un modello più complesso non riuscirebbe a fornire per le difficoltà, analitiche o computazionali, che insorgerebbero nel trattarlo. E' tuttavia importante che le ipotesi sulle quali il modello si basa vengano apertamente dichiarate per mettere in guardia su possibili limiti delle conclusioni a cui l'analisi del modello ha portato, in vista di eventuali raffinamenti successivi.
- Eventi rari possono accadere
- Un errore in cui incorre spesso il senso comune è quello di equiparare eventi rari, cioè eventi a cui è associata una probabilità bassa di verificarsi, ad eventi impossibili. Il fatto che una determinata persona vinca ad una lotteria nazionale è sicuramente un evento raro, ma se la sua vincita venisse considerata impossibile si dovrebbe considerare impossibile la vincita da parte di chiunque altro (perché l’estrazione dovrebbe fare preferenze?) e di conseguenza si dovrebbe ritenere impossibile che ci sia un vincitore della lotteria, il che è assurdo.
- D’altra
parte, il fatto che eventi rari prima o poi si verifichino potrebbe essere
poco interessante ai fini pratici, se il tempo di attesa è molto elevato.
Nel caso sopra citato, della lotteria annuale, la probabilità di vincere
acquistando un biglietto, se la lotteria vende dieci milioni di biglietti
è pari a :
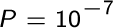
- (dovendo supporre che tutti i biglietti abbiano la stessa probabilità di essere estratti, altrimenti ci sarebbero gli estremi per azioni in sede giudiziaria!); supponendo che un individuo compri un biglietto tutti gli anni, il tempo medio di attesa per la sua vincita risulta pari a 10 milioni di anni, il che dovrebbe scoraggiarlo dallo spendere i soldi del biglietto!
- La stima della probabilità di un
evento è uno strumento fondamentale della statistica. Nelle sue
forme più semplici, si fonda sul calcolo combinatorio.
Anche se il risultato di ogni singolo
tentativo è imprevedibile, con un numero elevato di ripetizioni
si stabiliscono
regolarità che possono essere previste e calcolate. Dal punto
di vista
didattico, l’associazione del concetto di probabilità al
calcolo combinatorio è
un aspetto importante: serve per collegare una scelta, alla
probabilità con la
quale l'evento atteso può avvenire, nel contesto di tutti gli
eventi
alternativi possibili. E’ la base dell’inferenza
statistica, della scelta scientifica in tutti i casi d’incertezza.
Per risolvere i problemi probabilistici mediante il Calcolo combinatorio si considerano le situazioni con tutti gli eventi studiati equiprobabili.
Esempio:
Quando abbiamo definito la probabilità, abbiamo visto che, la probabilità del verificarsi di un evento A, è:
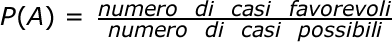
oppure:
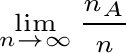 dove
dove 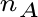 è
il numero di prove nelle quali si è verificato A,
è
il numero di prove nelle quali si è verificato A, 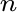 è il
numero totale di ripetizioni della stessa prova.
è il
numero totale di ripetizioni della stessa prova. - Dunque si devono contare il numero di prove.
- Questi calcoli di solito si fanno a posteriori, nulla evita di chiedersi a priori, cioè prima di eseguire l’esperimento, qual è la probabilità di ottenere un certo numero di successi, e quindi una certa frequenza. Si consideri il seguente esempio:
Un dado viene lanciato 4 volte. Qual è la probabilità che esca tre volte la faccia numero 1 e una volta un numero diverso da 1?
L’evento, che viene indicato con H, consta di due eventi parziali:
A: uscita del numero 1; Ā: uscita di un numero diverso da 1.
Il numero dei casi favorevoli dell’evento A è 1, quello dell’evento Ā è 5. Infatti sono proprio cinque i numeri del dado diversi da 1, per semplicità si pone:
p = P(A)= 1/6 , q = 1- p = P(Ā) = 1- P(A) = 5/6.
I due eventi A e Ā sono indipendenti e complementari, ossia l’evento unione A ∪ Ā è un evento certo.
Perché si verifichi l’evento H, l’evento A si deve verificare tre volte e l’evento contrario Ā una volta soltanto.
- Il problema può essere posto anche nel seguente modo:
- lanciando contemporaneamente quattro dadi, qual è la probabilità che si presentino tre facce contrassegnate dal numero 1 e una con un numero diverso da 1?
L'evento H si verifica al verificarsi di uno qualsiasi dei seguenti eventi intersezione:
A∩A∩A∩Ā, A∩A∩Ā∩A, A∩Ā∩A∩A, Ā∩A∩A∩A
Gli eventi sono indipendenti e dunque abbiamo:
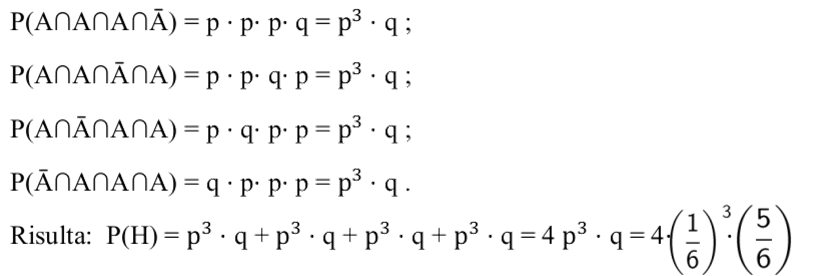
Gli esponenti 3 e 1 delle due potenze indicano quante volte si devono ripetere rispettivamente gli eventi di probabilità 1/6 e 5/6.
Il numero 4 che moltiplica le due potenze rappresenta il numero di tutti i raggruppamenti dei sei numeri di un dado che contengono tre volte 1 e una volta un numero diverso da 1.
Nell’esempio svolto, la determinazione del numero 4 è stata abbastanza semplice. Se, invece, si effettuano molti lanci, il calcolo del numero dei raggruppamenti in cui si presenta un certo numero di volte un evento diventa laborioso. Per esempio, volendo calcolare la probabilità che su 20 lanci di un dado esca 12 volte il numero 4 e 8 volte uno diverso da 4 bisogna effettuare il prodotto:
k ⋅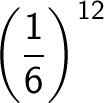 ·
· 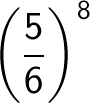
dove k indica il numero di tutti i raggruppamenti composti da dodici numeri uguali a 4 e otto numeri diversi da 4.
Per semplificare il calcolo del numero k, vengono introdotti i concetti di fattoriale di un numero naturale e di coefficiente binomiale, che saranno spiegati nella scheda:" Cenni di calcolo combinatorio"
Vedremo che il numero k sarà il coefficiente binomiale:
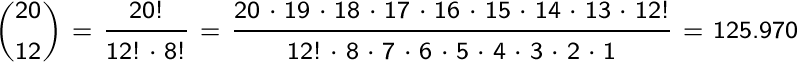

 Torna all'Indice
Torna all'Indice  pagina successiva
pagina successiva