Esempio 1

Siano date le funzioni

Calcolare il limite:

Risoluzione

E’ chiaro che:

,

per cui applicando il teorema sulla somma dei limiti avremmo

una forma indeterminata .

Ma possiamo risolvere il limite così:

Esempio 2

Siano date le funzioni:

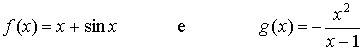
Calcolare il limite:

Risoluzione

Si ha:

per cui applicando il teorema sulla somma dei limiti

avremmo una forma indeterminata.

Risolvendo otteniamo invece:

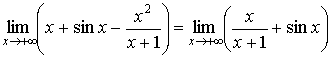
non esiste, poiché

Esempio 3

Siano date le funzioni

Calcolare il limite:

Risoluzione

Si ha:

per cui applicando il teorema sul prodotto dei limiti

avremmo una forma indeterminata.

Mentre, risolvendo, il limite del prodotto risulta:

Esempio 4

Siano date le funzioni

Calcolare il limite:

Risoluzione

Si ha:

per cui applicando il teorema sul prodotto dei limiti

avremmo una forma indeterminata.

Mentre , risolvendo, il limite del prodotto risulta:

Esempio 5

Determinare il limite per x tendente a + ¥ delle seguenti funzioni fratte:

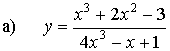
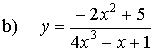
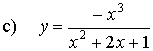
a) Risolvendo separatamente il limite del numeratore e

quello del denominatore otterremmo una forma indeterminata.

Allora, riscriviamo la funzione ponendo in evidenza x³ a numeratore e

a denominatore e poi semplificando:

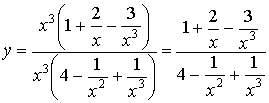
Quando x tende a , i termini che contengono una potenza di x

a denominatore tendono a 0;

quindi:

.

b)Mettiamo in evidenza x² a numeratore e a denominatore e

semplifichiamo

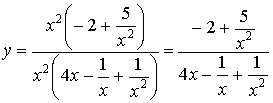
Quando x tende , i termini con x a denominatore tendono a 0;

y tende a diventare il quoziente tra

un numero costante (-2) e una grandezza via via crescente:

tende quindi a 0:

c)Analogamente ai casi precedenti scriviamo:

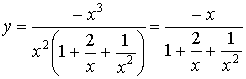
Per x tendente + ¥ otteniamo il quoziente tra –x

(via via più grande in valore assoluto) e 1:

la funzione tende, quindi, a :