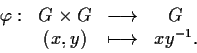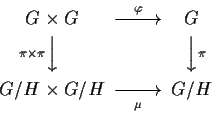Proposizione 2
Sia
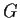
un gruppo topologico e sia
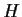
un suo sottogruppo
normale.
Lo spazio omogeneo
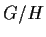
con la topologia quoziente è un gruppo
topologico.
Dimostrazione
Sappiamo che 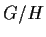 è uno spazio topologico, e che
è un gruppo (proposizione 3
della sezione "Gruppo quoziente").
è uno spazio topologico, e che
è un gruppo (proposizione 3
della sezione "Gruppo quoziente").
Proviamo che l'applicazione
è continua.
Sia
un
aperto di
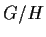
e sia
Mostriamo che
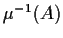
è intorno di ogni suo punto.
Consideriamo il seguente
diagramma commutativo:
dove
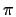
è la proiezione
di
in
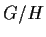
.
Sia
![$([a],[b])\in \mu^{-1}(A)$](img11.gif)
,
cioè
![$[a][b]^{-1}\in A$](img12.gif)
;
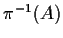
è un aperto di
e
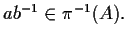
Allora
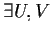
aperti di
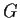
tali che
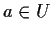
,
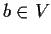
e
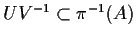
;
quindi
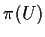
e
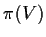
sono due aperti di
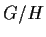
e
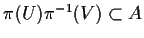
.
Da questo segue allora che
![$([a],[b])\in\pi(U)\times \pi(V)\subset
\mu^{-1}(A)$](img22.gif)
.
![]() è uno spazio topologico, e che
è un gruppo (proposizione 3
della sezione "Gruppo quoziente").
è uno spazio topologico, e che
è un gruppo (proposizione 3
della sezione "Gruppo quoziente").
![\begin{displaymath}\begin{array}{cccc}\mu:& G/H\times G/H&\longrightarrow&G/H\\ &
([x],[y])&\longmapsto&[x][y]^{-1}\end{array}\end{displaymath}](img5.gif)