Esempi 6
- 1)
-
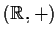 ,
,
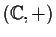 sono gruppi topologici: le applicazioni
sono gruppi topologici: le applicazioni
sono
continue.
- 2)
-
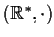 ,
,
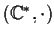 sono gruppi topologici: le applicazioni
sono gruppi topologici: le applicazioni
sono funzioni continue.
- 3)
-
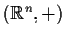 ,
,
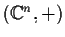 sono gruppi
topologici, essendo il prodotto di
sono gruppi
topologici, essendo il prodotto di 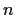 copie di
copie di
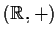 e
e
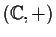 rispettivamente.
rispettivamente.
- 4)
- Ogni gruppo con la topologia
discreta è un gruppo topologico.
- 5)
- L'insieme
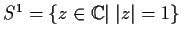 è un sottogruppo di
è un sottogruppo di
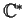 ,
e quindi con la
topologia di sottospazio indotta da
,
e quindi con la
topologia di sottospazio indotta da
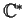 è un gruppo topologico.
è un gruppo topologico.
- 6)
- Sia
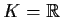 o
o
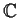 .
Si consideri l'applicazione biunivoca
.
Si consideri l'applicazione biunivoca
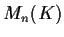 con la topologia indotta da
con la topologia indotta da 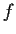 è uno spazio topologico e
è uno spazio topologico e 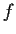 è
un omeomorfismo.
è
un omeomorfismo.
Il gruppo 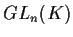 con il prodotto righe per colonne, con
la topologia indotta da
con il prodotto righe per colonne, con
la topologia indotta da 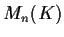 è un gruppo topologico: le applicazioni
è un gruppo topologico: le applicazioni
sono continue in quanto le 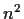 componenti
sono funzioni continue di
componenti
sono funzioni continue di 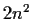 e
e 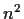 variabili (reali o complesse)
rispettivamente.
variabili (reali o complesse)
rispettivamente.
- 7)
- I gruppi lineari
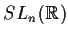 ,
,
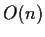 ,
,
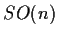 ,
,
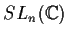 ,
,
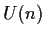 ,
,
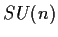 con la topologia indotta
da
con la topologia indotta
da 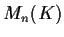 ,
dove
,
dove
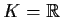 o
o
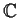 ,
sono gruppi topologici, essendo
sottogruppi del gruppo topologico
,
sono gruppi topologici, essendo
sottogruppi del gruppo topologico 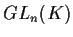 .
.
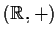 ,
,
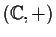 sono gruppi topologici: le applicazioni
sono gruppi topologici: le applicazioni
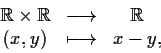
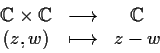
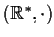 ,
,
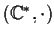 sono gruppi topologici: le applicazioni
sono gruppi topologici: le applicazioni
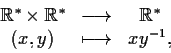
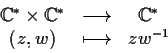
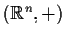 ,
,
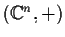 sono gruppi
topologici, essendo il prodotto di
sono gruppi
topologici, essendo il prodotto di 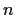 copie di
copie di
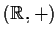 e
e
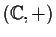 rispettivamente.
rispettivamente.
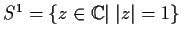 è un sottogruppo di
è un sottogruppo di
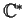 ,
e quindi con la
topologia di sottospazio indotta da
,
e quindi con la
topologia di sottospazio indotta da
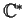 è un gruppo topologico.
è un gruppo topologico.
 o
o
 .
Si consideri l'applicazione biunivoca
.
Si consideri l'applicazione biunivoca
 con la topologia indotta da
con la topologia indotta da 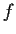 è uno spazio topologico e
è uno spazio topologico e 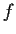 è
un omeomorfismo.
è
un omeomorfismo.
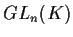 con il prodotto righe per colonne, con
la topologia indotta da
con il prodotto righe per colonne, con
la topologia indotta da 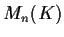 è un gruppo topologico: le applicazioni
è un gruppo topologico: le applicazioni
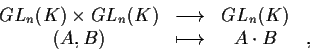
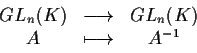
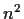 componenti
sono funzioni continue di
componenti
sono funzioni continue di 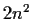 e
e 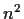 variabili (reali o complesse)
rispettivamente.
variabili (reali o complesse)
rispettivamente.
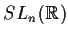 ,
,
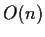 ,
,
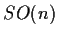 ,
,
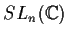 ,
,
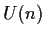 ,
,
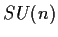 con la topologia indotta
da
con la topologia indotta
da 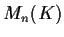 ,
dove
,
dove
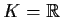 o
o
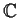 ,
sono gruppi topologici, essendo
sottogruppi del gruppo topologico
,
sono gruppi topologici, essendo
sottogruppi del gruppo topologico 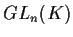 .
.
