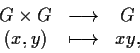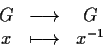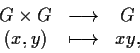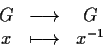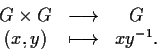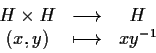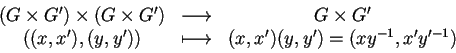Definizione 1
Un
gruppo topologico è un insieme
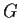
dotato di una struttura di
gruppo e di una topologia,
tali che le due applicazioni
siano continue.
In questo caso si dice che le due strutture, di gruppo e
topologica, sono compatibili.
Osservazione 2
Le due applicazioni della
definizione 1
sono continue se e solo se è
continua l'applicazione
Osservazione 3
Sia
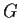
un gruppo topologico. Un sottogruppo
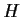
di
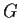
,
con la topologia di sottospazio, è un gruppo topologico.
Infatti la funzione
è continua essendo la
restrizione di una funzione continua.
Proposizione 4
Se
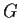
e
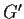
sono gruppi topologici, il gruppo prodotto
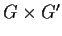
con la topologia
prodotto è un gruppo topologico.
Dimostrazione
L'applicazione
è
continua essendo ogni componente continua.
Notazione 5
In seguito quando considereremo
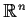
e
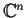
come spazi topologici, sottointenderemo la topologia euclidea.