Soluzione
Nel completamento proiettivo di
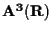 il problema si riduce al
problema di trovare una retta congiungente due punti dati.
il problema si riduce al
problema di trovare una retta congiungente due punti dati.
Infatti si consideri il punto
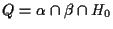 (dove
(dove 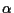 e
e
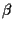 sono le chiusure proiettive rispettivamente di
sono le chiusure proiettive rispettivamente di 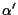 e
e 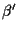 ).
).
La retta passante per 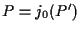 e
e 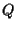 è quella richiesta.
è quella richiesta.
Nel caso particolare, passando a coordinate omogenee, abbiamo
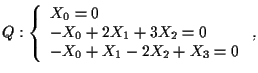 cioè
cioè
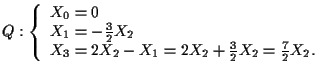
Quindi
![$Q=[0,-3,2,7],$](img34.gif) mentre
mentre
![$P=j_0(P')=[1,1,0,1].$](img35.gif)
La retta 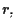 cioè la chiusura proiettiva di
cioè la chiusura proiettiva di 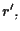 ha pertanto equazioni
cartesiane ottenute annullando i minori di ordine 3 orlati di
ha pertanto equazioni
cartesiane ottenute annullando i minori di ordine 3 orlati di
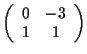 in
in
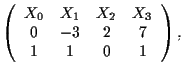 e cioè
e cioè
Pertanto
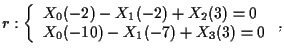 cioè
cioè
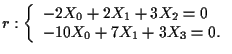 Quindi, passando a coordinate non omogenee,
Quindi, passando a coordinate non omogenee,
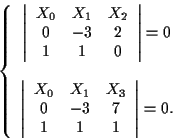
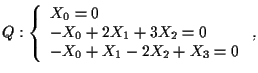 cioè
cioè
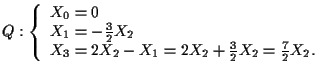
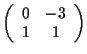 in
in
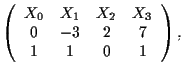 e cioè
e cioè
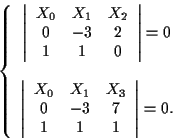
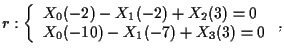 cioè
cioè
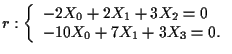 Quindi, passando a coordinate non omogenee,
Quindi, passando a coordinate non omogenee,
