Soluzione
Secondo la definizione 7,
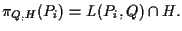 Vediamo allora di
ottenere quest'intersezione nei singoli casi:
Vediamo allora di
ottenere quest'intersezione nei singoli casi:
a) Le equazioni parametriche di 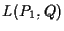 sono:
sono:
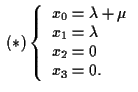
Sostituendo nell'equazione di 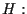
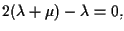 cioè
cioè
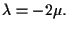 Tornando a sostituire in
Tornando a sostituire in 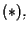 otteniamo
otteniamo
![$\pi_{Q,H}(P_1)=[1,2,0,0].$](img18.gif)
b) Le equazioni parametriche di 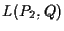 sono:
sono:
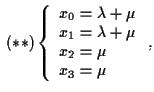 quindi equazioni cartesiane sono
quindi equazioni cartesiane sono
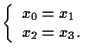
Sostituendo nell'equazione di 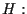
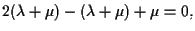 cioè
cioè
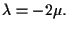 Tornando a sostituire in
Tornando a sostituire in
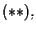 otteniamo
otteniamo
![$\pi_{Q,H}(P_2)=[1,1,-1,-1].$](img24.gif)
c) Le equazioni parametriche di 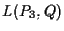 sono:
sono:
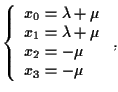 quindi equazioni cartesiane sono
quindi equazioni cartesiane sono
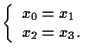
Questo significa che
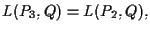 pertanto
pertanto
![$\pi_{Q,H}(P_3)=\pi_{Q,H}(P_2)=[1,1,-1,-1]=P_3.$](img28.gif)
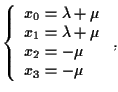 quindi equazioni cartesiane sono
quindi equazioni cartesiane sono
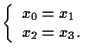
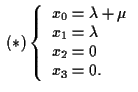
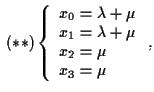 quindi equazioni cartesiane sono
quindi equazioni cartesiane sono
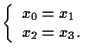
![]() sono:
sono:
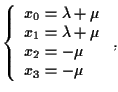 quindi equazioni cartesiane sono
quindi equazioni cartesiane sono
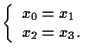
![]() pertanto
pertanto
![]()
