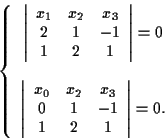
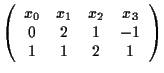Soluzione
La retta $r$ corrisponde al sottospazio vettoriale di $\mathbf{R^4}$ generato da $(0,2,1,-1)$ e $(1,1,2,1),$ che sono vettori linearmente indipendenti. Il vettore $(x_0, x_1, x_2, x_3)$ appartiene a tale sottospazio vettoriale se e solo se la matrice $\left( \begin{array}{cccc} x_0 & x_1 & x_2 & x_3\\ 0 & 2 & 1 & -1\\ 1 & 1 & 2 & 1 \end{array} \right)$ha rango 2, pertanto devono annullarsi i minori di rango 3. Questo accade se e solo se tutti i minori orlati di una sottomatrice quadrata di rango 2, per esempio di 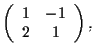$\left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right),$ sono nulli, quindi deve essere:


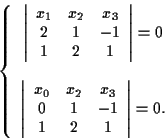
\begin{displaymath}\left\{ \begin{array}{c} \left\vert \begin{array}{ccc} x_1 & ... ...1 \\ 1 & 2 & 1 \end{array} \right\vert =0. \end{array}\right.\end{displaymath}

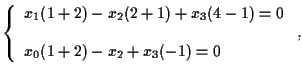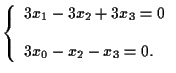
Equazioni per la retta sono pertanto $\left\{ \begin{array}{l} x_1(1+2)-x_2(2+1)+x_3(4-1)=0 \\ \\ x_0(1+2)-x_2+x_3(-1)=0 \end{array} \right.,$ cioè $\left\{ \begin{array}{l} 3x_1 -3x_2 +3x_3 =0 \\ \\ 3x_0 -x_2 -x_3 =0. \end{array} \right.$
TORNA ALLA TEORIA