13.2
Poiché le giaciture di 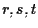 sono distinte abbiamo che esistono
sono distinte abbiamo che esistono
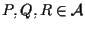 tali che
tali che
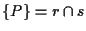
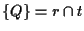
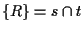 e tali punti non possono essere chiaramente collineari e quindi sono indipendenti.
e tali punti non possono essere chiaramente collineari e quindi sono indipendenti.
Identicamente esistono
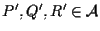 tali che
tali che
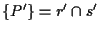
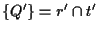
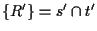 e tali punti di nuovo risulteranno indipendenti.
e tali punti di nuovo risulteranno indipendenti.
Esiste quindi un'unica affinità 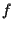 tale che
tale che 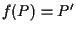 ,
,
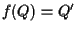 e
e 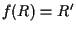 .
.
L'applicazione 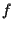 fa al caso nostro, infatti poichè
fa al caso nostro, infatti poichè 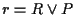 ,
,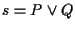 ,
,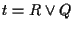 ,
e
,
e
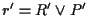 ,
,
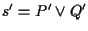 ,
,
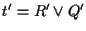 allora
allora 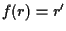 ,
,
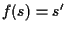 ,
,
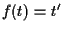 .
.

