7.
Vogliamo trovare la formula del cambiamento di coordinate dal riferimento
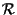 al riferimento
al riferimento
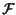 e tal fine dobbiamo quindi calcolare le coordinate -affini-
e tal fine dobbiamo quindi calcolare le coordinate -affini- 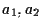 di
di 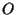 nel riferimento
nel riferimento
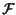 ossia le coordinate
ossia le coordinate 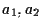 del vettore
del vettore
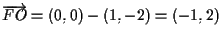 rispetto alla base
rispetto alla base
 .
.
A questo punto potremmo procedere risolvendo il sistema nelle incognite 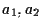

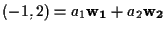 .
In questo caso la risoluzione è immediata, ma questa non è la strada piú indicata per risolvere il nostro problema; infatti in ogni caso dobbiamo trovare la matrice
.
In questo caso la risoluzione è immediata, ma questa non è la strada piú indicata per risolvere il nostro problema; infatti in ogni caso dobbiamo trovare la matrice
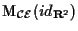 di passaggio dalla base canonica alla base
di passaggio dalla base canonica alla base
 ,
e tale matrice ci permette di trovare le coordinate di ogni vettore di
,
e tale matrice ci permette di trovare le coordinate di ogni vettore di
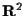 rispetto a
rispetto a
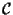 note le coordinate rispetto a
note le coordinate rispetto a
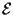 ,
in particolare ci permette di trovare le coordinate del vettore
,
in particolare ci permette di trovare le coordinate del vettore
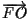 .
.
Come sempre in questi casi si scrive la matrice
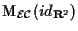 e questo è imediato:
e questo è imediato:
e si utilizza poi il fatto che
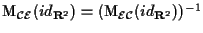 .
.
L'inversa risulta essere
e di qui troviamo le coordinate di
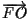 rispetto a
rispetto a
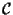 :
:
per cui potremo dire che le equazioni cercate sono
Facciamo una verifica: prendiamo ad esempio il punto 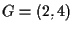 ,
esso ha coordinate rispetto al riferimento standard
,
esso ha coordinate rispetto al riferimento standard 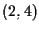 e tramite le formule trovate sopra otteniamo che le coordinate rispetto a
e tramite le formule trovate sopra otteniamo che le coordinate rispetto a
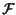 sono
sono
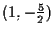 ;
verifichiamo direttamente che il vettore
;
verifichiamo direttamente che il vettore
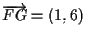 ha tali coordinate rispetto alla base
ha tali coordinate rispetto alla base
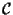 ;
cioè deve valere
;
cioè deve valere
e cosí è.
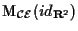 di passaggio dalla base canonica alla base
di passaggio dalla base canonica alla base
